使用Chrome浏览器效果最佳，继续浏览，你可能不会看到最佳的展示效果，

确定继续浏览么?

复制成功，请在其他浏览器进行阅读

基于优化窗函数改进S变换的低频振荡暂态检测方法

- ORCID：
江青柳 ¹
✉
- ORCID：
梁成斌 ¹
✉
- ORCID：
陈光贵 ²
- ORCID：
王嵘瑜 ²
- ORCID：
贺青 ³

1. 贵州大学电气工程学院，贵州贵阳 550025； 2. 贵州省计量测试院，贵州贵阳 550025； 3. 中国计量科学研究院电磁计量科学研究所，北京 100029

中图分类号： TB971

最近更新：2025-02-06

DOI： 10.3969/j.issn.1000-1158.2025.01.21

摘要

低频振荡暂态是电力系统中常见的一种电能质量扰动，其直接影响电力系统的安全、稳定运行。通过对影响时频分析算法检测精度的窗函数进行了研究，提出一种基于优化窗函数改进S变换的低频振荡暂态检测方法。首先，对时频分析算法中窗函数随检测频率变化的改变特性进行分析，确定了适用于低频振荡暂态扰动检测的优化窗函数，并利用其构造了改进S变换算法；其次，通过利用卷积定理、Fourier变换及其逆变换，推导了改进S变换算法快速实现的计算表达式，获取了包含信号幅值、相位信息的二维时频矩阵，给出了改进算法的实现流程；最后，采用包含低频振荡暂态扰动的电网信号对改进算法进行了测试。该优化算法对低频振荡暂态扰动表现出相对最佳的时频能量聚集性能，实际实验中所测得扰动中心频率为600 Hz，与扰动的生成频率相吻合，验证了改进算法的可行性和有效性。

关键词

电磁计量; 电能质量扰动; 改进S变换; 低频振荡暂态; 窗函数优化; 时频能量聚集

1 引言

振荡暂态是一种常见的暂态电能质量扰动，是指在稳态状态下，电压或电流发生的有正负极性、非工频的振荡衰减变化现象。低频振荡瞬态（low frequency oscillation transient， LFOT）是输配电系统中的一种典型暂态现象。IEEE Std 1159-2019^［

1］根据电网信号频谱范围，将频率小于5 kHz，持续时间在0.3~50 ms，典型幅度为0~4 p.u.的振荡暂态定义为LFOT，p.u.（per-unit value）为标幺值。LFOT扰动主要由配电网中铁磁共振和变压器充电产生的励磁涌流产生^{［参考文献 2

百度学术}2］，可能造成运行设备的绝缘破坏，导致电子设备损坏，影响电力系统安全、稳定运行。LFOT频率高、持续时间短，采用信号时频分析方法对含有LFOT的电网信号进行分析，获取其扰动频率、扰动强度、起止时刻和持续时间等信息，是LFOT监测和治理的前提和基础，也是加强智能电网状态感知的重要途径^{［参考文献 3-5}3-5］。

信号时频分析方法将信号的时域和频域特性相结合，能提供更全面的信号信息^［

6］。典型的时频分析方法包括短时Fourier变换（short-time Fourier transform，STFT）、小波变换（wavelet transform，WT）、S变换（stockwel transform，ST）等。STFT在Fourier变换^{［参考文献 7

百度学术}7，8］基础上引入时间相关窗函数的概念，采用窗函数将待测信号在时域分成若干间隔，然后用Fourier变换对每个间隔进行分析以确定该时间间隔的频率成分，其处理方法为对信号作用一个滑动窗函数，再进行Fourier变换运算，具备时频局部特性^{［参考文献 9

百度学术}9，10］。

然而，STFT虽在一定程度上克服了Fourier变换不能对信号进行时频分析的缺陷^［

11，12］，但其窗函数的大小和形状均为固定不变，针对不同检测频率其窗函数不能发生针对性改变，导致变换结果中时频分辨率不可调节，同时，也受频谱泄漏和栅栏效应影响，实际应用中的适应性较差^{［参考文献 13

百度学术}13，14］。WT通过将信号分解为一系列小波函数的叠加来获得时频分析能力，可通过伸缩和平移等运算功能对信号进行多尺度的细化分析，具有多尺度分析的特点^{［参考文献 15

百度学术}15］，可以实现扰动信号的多分辨率分析^{［参考文献 16

百度学术}16］。但时频分析的效果与母小波的选择、采样频率和分解层数密切相关，如果相关参数选择不当，会造成较大的检测误差，且受噪声影响较大，不能直接得到扰动信号的幅值、频率等信息^{［参考文献 17

百度学术}17，18］。

ST是在STFT和WT的基础上发展而来的可逆时频分析方法^［

19，20］，采用与时间和频率相关的Gaussian窗函数作为积分变换的核函数，其窗函数可随检测频率的变化而调整其窗形宽度和高度，从而为变换算法提供可变分辨率，克服了STFT窗函数宽度和高度确定以及时频分辨率不足的缺陷^{［参考文献 21

百度学术}21］。同时，ST可视为WT算法的相角校正，不必满足WT的小波容许条件^{［参考文献 22

百度学术}22］。

然而，ST中使用的Gaussian窗函数在较低频率处能够提供较佳的频率分辨率，随着检测频率的逐渐增大，其频率分辨率逐渐恶化，频谱泄漏现象严重，导致对于振荡暂态、谐波等扰动的频率检测能力不足^［

23，24］。因此，本文从窗函数性能优化入手，确定有利于LFOT扰动检测的Gaussian窗函数，进一步构造改进S变换算法，并推导改进算法的快速实现方法。

2 改进S变换算法

2.1　ST原理

对信号x（t）进行时频分析，其ST的表达式^［

21］为：

S (τ, f) = \int_{- \infty}^{+ \infty} x (t) w (τ - t, f) e^{- j 2 π f t} d t

（1）

式中：w（τ-t，f）为与检测频率相关的Gaussian窗函数，τ为时移因子，是控制Gaussian窗在时间轴位置的参数，通过调节τ的大小，获取信号的局部频谱信息，f为频率，t为时间。

w（τ-t，f）可表示为：

w (τ - t, f) = \frac{|f|}{\sqrt[]{2 π}} e^{\frac{- f^{2} {(τ - t)}^{2}}{2}}

（2）

由式（2）可知，ST中Gaussian窗函数窗形随检测频率升高而逐渐变窄，其时频分辨率逐渐由频率分辨率更佳向时间分辨率更佳过渡，不利于对复杂电网信号基波幅值和高频扰动频率检测。

2.2　改进S变换算法

2.2.1　优化Gaussian窗函数

为提高ST算法复杂电网信号基波幅值检测精度，文献［

23］对ST中提供时频分辨能力的Gaussian窗函数进行了研究，设计了调节能力更强的双参数优化Gaussian窗函数，具体表达式为：

w_{g} (t, f) = \frac{1}{ρ (f) \sqrt[]{2 π}} e^{\frac{- t^{2}}{2 ρ^{2} (f)}}

（3）

其中，标准差控制函数ρ（f）可表示为：

ρ (f) = |γ_{1} f + γ_{2}|

（4）

式中：γ₁≥0和γ₂>0为窗函数控制调节参数。

在低频段50 Hz基波频率下，所设计的优化Gaussian窗函数能提供更优的时间分辨率，有利于算法对电压暂降、暂升、中断、闪变等特征表现为基波幅值波动扰动的幅值准确测量。LFOT的扰动频率通常为电网基波频率的数十倍，在使用时频分析算法对LFOT的检测过程中，较高的频率分辨率有利于对扰动频率的确定。因此，对窗函数（3）中ρ（f）的控制参数γ₁和γ₂进行分析，确定其对窗函数变化特性的影响。

调节参数γ₁和γ₂对控制函数值ρ（f）影响不同，但是最终Gaussian窗函数的窗形时频特性，是通过调节参数γ₁和γ₂与检测频率f共同影响ρ（f）的值来改变。图1为γ₁对Gaussian优化窗函数窗形的影响，窗函数窗形随着γ₁的增大而快速变宽。图2为γ₂对Gaussian优化窗函数窗形的影响，窗函数窗形随着γ₂的增大而逐步变宽。

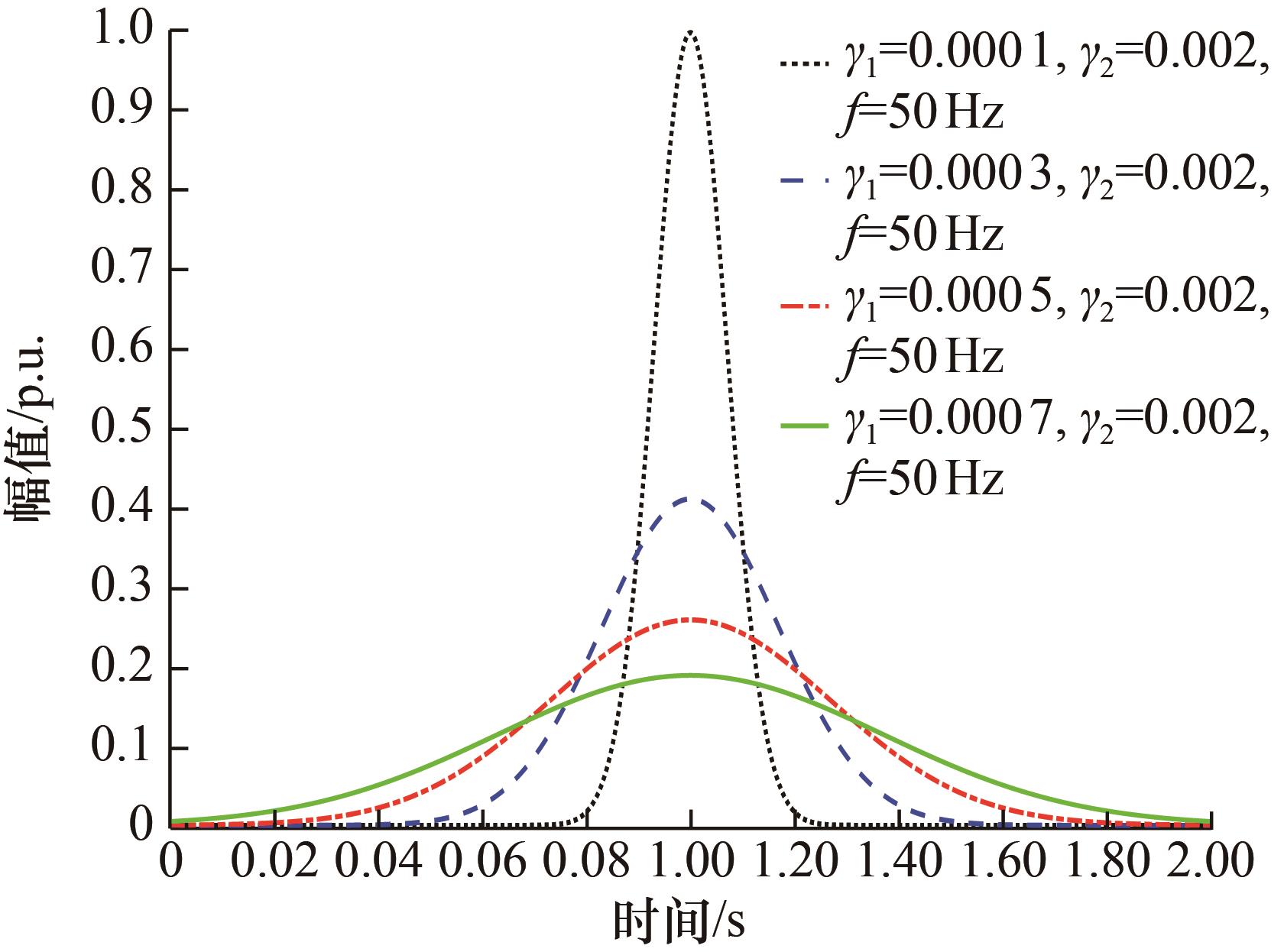
图1 γ₁对优化Gaussian窗的影响

Fig.1 Effect of different γ₁ on optimized Gaussian windows

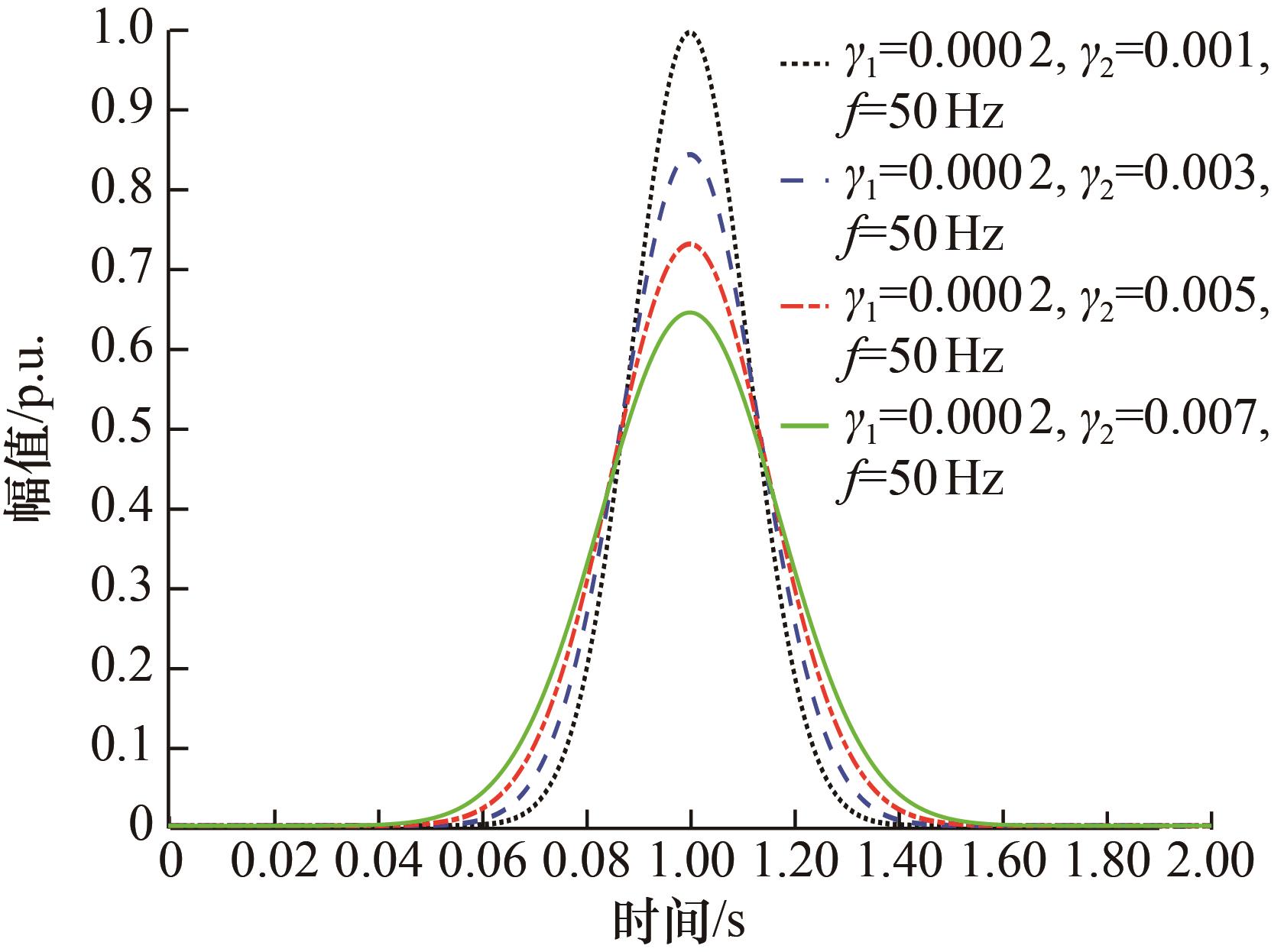
图2 γ₂对优化Gaussian窗的影响

Fig.2 Effect of different γ₂ on optimized Gaussian windows

因此，式（3）所示优化窗函数能在低频频率处提供较高的时间分辨率，随着检测频率变大，分辨率会从时间分辨率较佳向频率分辨率更佳的方向变化，有利于对LFOT扰动频率的检测。

2.2.2　改进S变换算法设计

采用式（3）所示优化窗函数对式（1）所示ST进行改进，构造有利于LFOT扰动频率检测的改进S变换算法。对于给定的待测信号x（t）∈L²（ℝ），即信号x（t）为实数域上平方可积函数，其中ℝ为实数域，L²（ℝ）为ℝ上的平方可积函数，则其信号x（t）的改进S变换（MST）表达式为：

\begin{array}{l} M_{s} (τ, f) = \int_{- \infty}^{+ \infty} x (t) w_{g} (τ - t, f) e^{- j 2 π f t} d t \\ = \int_{- \infty}^{+ \infty} x (t) \frac{1}{ρ (f) \sqrt[]{2 π}} e^{\frac{- {(τ - t)}^{2}}{2 ρ^{2} (f)}} e^{- j 2 π f t} d t \\ = \int_{- \infty}^{+ \infty} x (t) \frac{1}{|γ_{1} f + γ_{2}| \sqrt[]{2 π}} e^{\frac{- {(τ - t)}^{2}}{2 {(γ_{1} f + γ_{2})}^{2}}} e^{- j 2 π f t} d t \end{array}

（5）

控制参数γ₁与窗控制函数ρ（f）是正相关线性关系，控制参数γ₂与ρ（f）是叠加关系。控制参数γ₁可调节Gaussian优化窗函数窗形随检测频率的改变速率，控制参数γ₂则可针对某固定频率下的时频分辨率进行微调。具体地，较大的γ₁值对应着相对较快的分辨率转换速率，增大γ₂的值则有利于算法向频率分辨率更优的方向过渡。

3 算法快速实现

3.1　MST的Fourier变换表达形式

为便捷实现MST算法，对MST变换式（5）的Fourier变换表达形式进行研究。

定理1 对给定的待测信号x（t）∈L²（ℝ），信号x（t）的MST式（5）可进一步由信号频移的Fourier变换结果表示为：

M_{s} (τ, f) = \int_{- \infty}^{+ \infty} X (σ + f) e^{- {(γ_{1} f + γ_{2})}^{2} 2 π^{2} σ^{2}} e^{j 2 π σ τ} d σ

（6）

证明：记x（t，f）=x（t）e^-j²^π^ft，则由信号x（t）的改进MST式（5）可得：

M_{s} (τ, f) = \int_{- \infty}^{+ \infty} x (t, f) w_{g} (τ - t, f) d t

（7）

其中： $w_{g} (τ - t, f) = \frac{1}{|γ_{1} f + γ_{2}| \sqrt[]{2 π}} e^{- \frac{{(τ - t)}^{2}}{2 {(γ_{1} f + γ_{2})}^{2}}}$ 。

式（7）可表达为卷积形式：

M_{s} (τ, f) = x (τ, f) * w_{g} (τ, f)

（8）

其中： $*$ 表示卷积运算。

将卷积运算式（8）等号左右两边同时作关于时间τ到频率σ的Fourier变换，可得：

H (σ, f) = X (σ, f) W_{g} (σ, f)

（9）

式（9）中的H（σ，f）表示为M_s（τ，f）的Fourier变换式：

H (σ, f) = \int_{- \infty}^{+ \infty} M_{s} (τ, f) e^{- j 2 π σ τ} d τ

（10）

式（9）中X（σ，f）表示为式（8）中x（τ，f）Fourier变换式：

\begin{array}{l} X (σ, f) = \int_{- \infty}^{+ \infty} x (τ, f) e^{- j 2 π σ τ} d τ \\ = \int_{- \infty}^{+ \infty} x (τ) e^{- j 2 π f τ} e^{- j 2 π σ τ} d τ \\ = \int_{- \infty}^{+ \infty} x (τ) e^{- j 2 π (σ + f) τ} d τ \\ = X (σ + f) \end{array}

（11）

式（9）中的W_g（σ，f）为式（8）中w_g（τ，f）的Fourier变换式：

\begin{array}{l} W_{g} (σ, f) = \int_{- \infty}^{+ \infty} w_{g} (τ, f) e^{- j 2 π σ τ} d τ \\ = \frac{1}{|γ_{1} f + γ_{2}| \sqrt[]{2 π}} \int_{- \infty}^{+ \infty} e^{- \frac{τ^{2}}{2 {(γ_{1} f + γ_{2})}^{2}} - j 2 π σ τ} d τ \\ = \frac{1}{|γ_{1} f + γ_{2}| \sqrt[]{2 π}} \\ \times \int_{- \infty}^{+ \infty} e^{- \frac{1}{2 {(γ_{1} f + γ_{2})}^{2}} {[τ + {(γ_{1} f + γ_{2})}^{2} j 2 π σ]}^{2} - {(γ_{1} f + γ_{2})}^{2} 2 π^{2} σ^{2}} d τ \\ = \frac{1}{|γ_{1} f + γ_{2}| \sqrt[]{2 π}} e^{- {(γ_{1} f + γ_{2})}^{2} 2 π^{2} σ^{2}} \\ \times \int_{- \infty}^{+ \infty} e^{- \frac{1}{2 {(γ_{1} f + γ_{2})}^{2}} {[τ + {(γ_{1} f + γ_{2})}^{2} j 2 π σ]}^{2}} d τ \end{array}

（12）

进一步，记：

η = \frac{1}{\sqrt[]{2} |γ_{1} f + γ_{2}|} (τ + {(γ_{1} f + γ_{2})}^{2} j 2 π σ)

（13）

则有

d τ = \sqrt[]{2} |γ_{1} f + γ_{2}| d η

（14）

结合式（13）、式（14）和Gaussian积分公式，式（12）可转变为：

\begin{array}{l} W_{g} (σ, f) = \frac{1}{|γ_{1} f + γ_{2}| \sqrt[]{2 π}} e^{- {(γ_{1} f + γ_{2})}^{2} 2 π^{2} σ^{2}} \int_{- \infty}^{+ \infty} e^{- η^{2}} d τ \\ = \frac{1}{|γ_{1} f + γ_{2}| \sqrt[]{2 π}} e^{- {(γ_{1} f + γ_{2})}^{2} 2 π^{2} σ^{2}} \\ \times \int_{- \infty}^{+ \infty} \sqrt[]{2} |γ_{1} f + γ_{2}| e^{- η^{2}} d η \\ = e^{- {(γ_{1} f + γ_{2})}^{2} 2 π^{2} σ^{2}} \end{array}

（15）

将式（11）和式（15）代入到式（9），可得：

H (σ, f) = X (σ + f) e^{- {(γ_{1} f + γ_{2})}^{2} 2 π^{2} σ^{2}}

（16）

对于H（σ， f）作关于频率σ到时间τ的逆Fourier变换，可得式（6）所描述的MST由Fourier变换表达的形式：

\begin{array}{l} M_{s} (τ, f) = \int_{- \infty}^{+ \infty} H (σ, f) e^{j 2 π σ τ} d σ \\ = \int_{- \infty}^{+ \infty} X (σ, f) e^{- {(γ_{1} f + γ_{2})}^{2} 2 π^{2} σ^{2}} e^{j 2 π σ τ} d σ \end{array}

（17）

综上，由MST表达式（6）可通过计算，得到信号MST的时频分布信息。

3.2　离散MST

在计算机或者信号处理过程中，对信号进行采样，设采样率为f_s，采样长度为N点，对信号x（t）∈L²（ℝ）进行均匀采样，采样时间间隔为T_s=1/f_s，对MST表达式及其由Fourier变换表示出的表达式进行离散化，记时移因子τ=mT，时间变量t=nT_s，以及频率变量f=k/（NT_s），m，n，k为0，1，2，…，N-1。

离散信号x［nT_s］的离散Fourier变换表达式为：

X [\frac{k}{N T_{s}}] = \sum_{n = 0}^{N - 1} x [n T_{s}] e^{- \frac{j 2 π k n}{N}}

（18）

将式（6）进行离散化处理，可得MST的离散表达式为：

\begin{array}{l} M_{s} [m T_{s}, \frac{k}{N T_{s}}] = \frac{1}{N} \sum_{l = 0}^{N - 1} X [\frac{l + k}{N T_{s}}] \\ \times e^{- {(\frac{γ_{1} k}{N T_{s}} + γ_{2})}^{2} 2 π^{2} {(\frac{1}{N T_{s}})}^{2}} e^{\frac{j 2 π l m}{N}} \end{array}

（19）

MST的离散Fourier变换表达形式（19）中，时频变换结果为时频二维矩阵，矩阵的列向量表示为某一频率下不同时间的幅值和相角信息，行向量则表示信号在某一时刻下不同频率的相关信息。MST变换的时频二维矩阵中每个元素均为复数形式，在某一频率下，对检测信号的幅值和相角信息进行提取，根据Euler公式，将式（19）按实部和虚部展开为：

\begin{array}{l} M_{s} [m T_{s}, \frac{k}{N T_{s}}] \\ = \frac{1}{N} \sum_{l = 0}^{N - 1} X [\frac{l + k}{N T_{s}}] e^{- {(\frac{γ_{1} k}{N T_{s}} + γ_{2})}^{2} 2 π^{2} {(\frac{l}{N T_{s}})}^{2}} c o s (\frac{2 π l m}{N}) \\ + j \frac{1}{N} \sum_{l = 0}^{N - 1} X [\frac{l + k}{N T_{s}}] e^{- {(\frac{γ_{1} k}{N T_{s}} + γ_{2})}^{2} 2 π^{2} {(\frac{l}{N T_{s}})}^{2}} s i n (\frac{2 π l m}{N}) \end{array}

（20）

其中，实部为

\begin{array}{l} R e \{M_{s} [m T_{s}, \frac{k}{N T_{s}}]\} \\ = \frac{1}{N} \sum_{l = 0}^{N - 1} X [\frac{l + k}{N T_{s}}] e^{- {(\frac{γ_{1} k}{N T_{s}} + γ_{2})}^{2} 2 π^{2} {(\frac{l}{N T_{s}})}^{2}} c o s (\frac{2 π l m}{N}) \end{array}

（21）

虚部为

\begin{array}{l} I m \{M_{s} [m T_{s}, \frac{k}{N T_{s}}]\} \\ = \frac{1}{N} \sum_{l = 0}^{N - 1} X [\frac{l + k}{N T_{s}}] e^{- {(\frac{γ_{1} k}{N T_{s}} + γ_{2})}^{2} 2 π^{2} {(\frac{l}{N T_{s}})}^{2}} s i n (\frac{2 π l m}{N}) \end{array}

（22）

进一步，根据MST的实部和虚部，利用幅值和相角提取公式，可得信号MST的模矩阵为：

\begin{array}{l} |M_{s} [m T_{s}, \frac{k}{N T_{s}}]| \\ = \sqrt[]{R e^{2} \{M_{s} [m T_{s}, \frac{k}{N T_{s}}]\} + I m^{2} \{M_{s} [m T_{s}, \frac{k}{N T_{s}}]\}} \end{array}

（23）

相角矩阵为：

\begin{array}{l} φ [m T_{s}, \frac{k}{N T_{s}}] \\ = a r c t a n [\frac{I m \{M_{s} [m T_{s}, \frac{k}{N T_{s}}]\}}{R e \{M_{s} [m T_{s}, \frac{k}{N T_{s}}]\}}] \end{array}

（24）

继而，可根据信号的幅值和相角矩阵实现任意检测时刻、任意检测频率下信号的幅值和相角信息，确定扰动频率、强度和时间。

3.3　MST快速实现方法

根据MST的Fourier变换表达形式（6）及其离散形式（19），MST快速实现流程可概述为

步骤1：对于长度为N，采样频率为f=1/T_s的待测信号x（t），计算其Fourier变换频谱序列 $X [\frac{l}{N T_{s}}]$ ，l=0，1，2，…，N-1；

步骤2：根据频率 $\frac{k}{N T_{s}}$ ，k=0，1，2，…，M-1，将序列 $X [\frac{l}{N T_{s}}]$ 进行频移至 $X [\frac{l + k}{N T_{s}}]$ ；

步骤3：计算频率 $\frac{k}{N T_{s}}$ ，k=0，1，2，…，M-1，下优化Gaussian窗的频谱向量 $W_{g} [\frac{l}{N T_{s}}, \frac{k}{N T_{s}}]$ ；

步骤4：将步骤2中频移序列向量 $X [\frac{l + k}{N T_{s}}]$ 与步骤3窗函数频谱向量 $W_{g} [\frac{l}{N T_{s}}, \frac{k}{N T_{s}}]$ 进行Hadamard积运算；

步骤5：对在步骤4得到的频谱乘积序列 $X [\frac{l + k}{N T_{s}}]$ 。 $W_{g} [\frac{l}{N T_{s}}, \frac{k}{N T_{s}}]$ 执行逆Fourier变换，得到频率 $\frac{k}{N T_{s}}$ 下的信号时域信息。

步骤6：对于k=0，1，2，…，M-1经行非敏感频率点剔除，重复步骤2到5，得到信号的MST二维时频矩阵 $M_{s} [m T_{s}, \frac{k}{N T_{s}}]$ ；

步骤7：根据二维时频矩阵，利用幅值和相角计算公式得出信号在任意频率、任意时刻的幅值和相角信息。

4 LFOT扰动信号测试

4.1　仿真测试

使用含有LFOT扰动的电网信号对MST算法进行测试，同时采用STFT和ST算法作为实验参照算法。测试在MATLAB环境进行，测试信号根据IEEE Std1159-2019电能质量标准进行生成。LFOT信号描述为正常信号和低频振荡扰动分量的叠加，表示为：

\begin{array}{l} x (t) = A s i n (2 π f_{0} t) + α e^{\frac{- (t - t_{1})}{ϕ}} \\ \times [ε (t - t_{1}) - ε (t - t_{2})] \\ \times A s i n [2 π f_{0} β (t - t_{1})] \end{array}

（25）

式中：A为正弦电压信号的幅值；角频率ω₀=2πf₀；f₀为工频信号，工频周期T=1/f₀；α为振荡暂态幅值控制参数，0.1≤α≤0.8；ϕ为振荡衰减控制参数，3 ms≤ϕ≤50 ms；t₁为振荡展台开始时刻；t₂为暂态结束时刻，0.5T≤t₁-t₂≤3T；β为振荡暂态的频率系数参数，6≤β≤18。测试信号参数中，采样率为10.24 kHz，采样长度为1 024点，γ₁和γ₂的取值分别为0.000 5和0.03，f₀=50 Hz，α=0.8，ϕ=0.01 s，t₁=0.02 s，t₂=0.05 s，β=16。

图3展示了STFT、ST和MST三种算法对LFOT扰动信号的检测结果。图3（a）~图3（c）为测试信号经3种算法时频分析后的时间‑频率‑幅值三维结果，可见，3种算法均检测到了低频振荡现象；图3（d）~图3（f）展示了3种算法的时频能量聚集性能，可见，MST能有效缓解LFOT扰动信号的频谱扩散现象，能量聚集性能相对最优；图3（g）为LFOT扰动测试信号时域图形；图3（h）为3种算法对电网扰动信号基波幅值的检测结果，由图3（h）可见，MST和ST的检测曲线几乎重合，较为准确地反映出了信号基波幅值情况；图3（i）为3种算法在t=0.04 s时刻对测试信号扰动频率的检测结果，可见，MST算法的频谱扩散现象最小，对LFOT扰动的频率检测结果最为准确。

图 3 MST及对照算法对LFOT信号的检测结果

Fig.3 Detection results of LFOT signals by MST and other control algorithms

4.2　实验测试

在仿真实验的基础上，搭建LFOT扰动检测实验平台，平台主要由信号发生器、数据采集模块、示波器和PC机组成，如图4所示。LFOT扰动信号由Agilent 33500B函数信号发生器生成，扰动频率为600 Hz。扰动信号生成后，由数据采集模块对信号进行采集，并经USB将采集数据输送到计算机进行信号分析，生成的扰动信号由示波器进行波形监测。

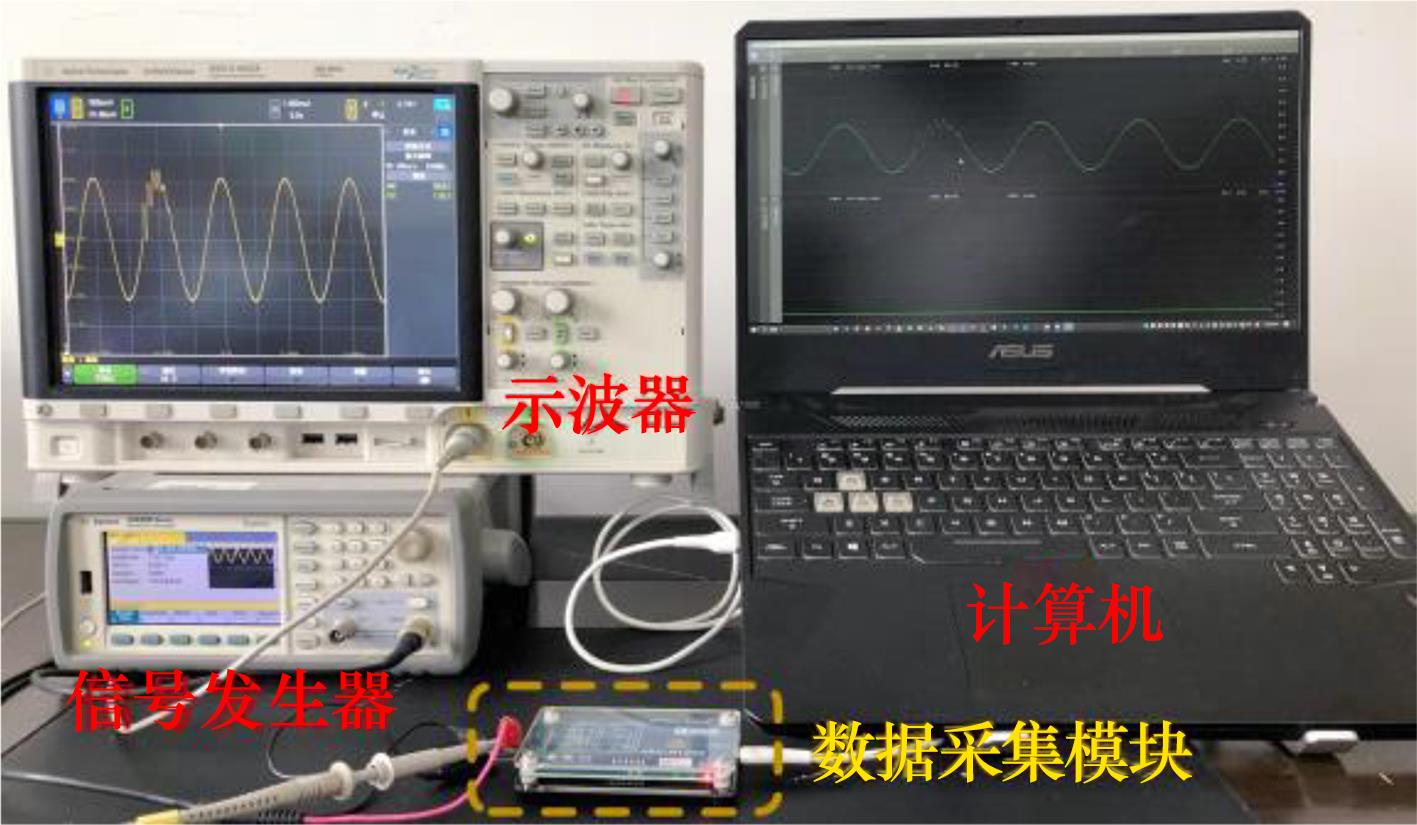
图4 实验测试平台

Fig.4 Experimental test platform

实验结果参见图5。图5（a）为所采集的测试信号，图5（b）为对LFOT扰动信号的时频幅值三维分析结果，可见，本文MST算法较为准确地反映出了信号的扰动情况，扰动发生时刻信号频谱对应的扰动频率为600 Hz，与所生成的扰动频率相符。

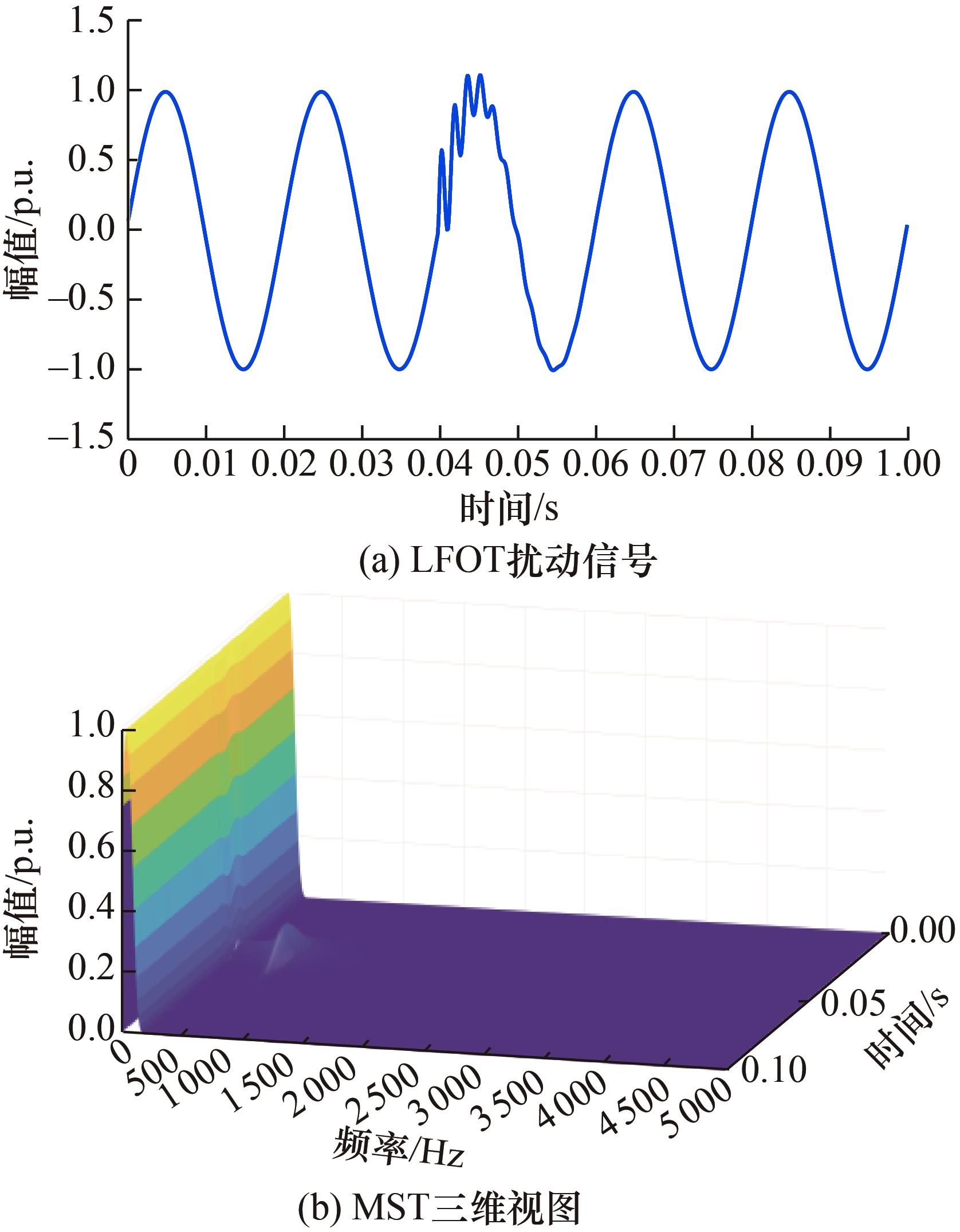
图 5 实验信号与结果

Fig.5 Experimental signals and results

5 结论

本文针对复杂电网信号中的低频振荡暂态扰动检测问题提出了一种基于优化窗函数改进S变换（MST）的检测方法，验证了所采用的优化窗函数更适用于低频振荡暂态扰动的频率检测，推导了有利于算法快速实现、由信号Fourier变换表出的算法表达式，给出了算法快速实现方法，利用扰动仿真信号和实际实验测试了所提方法的可行性和有效性，可为复杂电网信号分析、电力系统监测、电能科学计量提供参考和依据。

参考文献

IEEE Recommended Practice for Power Quality Data Interchange Format （PQDIF）：1159.3-2019［S］. 2019. [百度学术]

AZMAN S K， ISBEIH Y J， El MOURSI M S， et al. A Unified Online Deep Learning Prediction Model for Small Signal and Transient Stability［J］. IEEE Transactions on Power Systems， 2020， 35（6）： 4585-4598. [百度学术]

张鹏，毕天姝. HVDC引起次同步振荡暂态扰动风险的机理分析［J］. 中国电机工程学报， 2016， 36（4）： 961-968， 1178. [百度学术]

ZHANG P， BI T S. Mechanism Analysis of Large Disturbance Risk of Subsynchronous Oscillation caused by HVDC［J］. Proceedings of the CSEE， 2016， 36（4）： 961-968， 1178. [百度学术]

张立国，张淑清，李莎莎，等. 电能质量扰动识别的不同时频分析方法研究［J］. 计量学报， 2017， 38（3）： 345-350. [百度学术]

ZHANG L G， ZHANG S Q， LI S S， et al. Study on the Detection and Classification of Power Quality Disturbances Using Difference Time-frequency Methods［J］. Acta Metrologica Sinica， 2017， 38（3）： 345-350. [百度学术]

李艳，林晓明，赵宇明，等. 基于改进mSDFT算法的谐波信号提取方法［J］. 计量学报， 2024， 45（10）： 1435-1443. [百度学术]

LI Y， LIN X M， ZHAO Y M， et al. A Harmonics Signal Extraction Method Based on Improved mSDFT Algorithm［J］. Acta Metrologica Sinica， 2024， 45（10）： 1435-1443. [百度学术]

LI L， CAI H， JIANG Q， et al. An Empirical Signal Separation Algorithm for Multicomponent Signals Based on Linear Time-Frequency Analysis［J］. Mechanical Systems and Signal Processing， 2019， 121： 791-809. [百度学术]

BORKOWSKI J， MROCZKA J， MATUSIAK A， et al. Frequency Estimation in Interpolated Discrete Fourier Transform With Generalized Maximum Sidelobe Decay Windows for the Control of Power［J］. IEEE Transactions on Industrial Informatics， 2020， 17（3）： 1614-1624. [百度学术]

倪伟伦，顾丹珍，曹依烈，等. 基于改进S变换的非稳态信号的电能计量方法研究［J］. 电测与仪表， 2024， 61（5）： 175-181，224. [百度学术]

NI W L， GU D Z， CAO Y L， et al. Research on Electric Energy Measurement Method Based on Improved S-transform for Unsteady Signal［J］. Electrical Measurement & Instrumentation， 2024， 61（5）： 175-181，224. [百度学术]

陈正颖，王黎明，怡勇. 基于短时傅里叶变换的直流电晕无线电干扰激发电流计算［J］. 高电压技术， 2019， 45（6）： 1866-1872. [百度学术]

CHEN Z Y， WANG L M， YI Y. Computation of Radio Interference Excitation Current of DC Corona Based on Short-time Fourier Transform ［J］. High Voltage Engineering， 2019， 45（6）： 1866-1872. [百度学术]

郑海明，姚鹏辉. 基于协相关性和傅里叶变换-差分吸收光谱法的臭氧浓度在线测量研究［J］. 计量学报， 2023， 44（2）： 284-289. [百度学术]

ZHENG H M， YAO P H. Research of On-line Monitoring of Ozone Concentration Based on Association Correlation and Differential Optical Absorption Spectroscopy-Fourier Transform［J］. Acta Metrologica Sinica， 2023， 44（2）： 284-289. [百度学术]

袁小平，胡秀娟，孙英洲，等. 基于加窗傅里叶变换的弱电网阻抗测量算法［J］. 电力系统保护与控制， 2018， 46（10）： 96-101. [百度学术]

YUAN X P， HU X J， SUN Y Z， et al. A Weak Grid Impedance Detection Method Based on Windowed Fourier Transformation［J］. Power System Protection and Control， 2018， 46（10）： 96-101. [百度学术]

方旭，刘欣，李琪，等. 面向油品参数快速计量的高精度傅里叶近红外光谱仪［J］. 计量学报， 2024， 45（1）： 103-111. [百度学术]

FANG X， LIU X， LI Q， et al. High Precision Near Infrared Fourier Spectrometer for Rapid Measurement of Oil Parameters［J］. Acta Metrologica Sinica， 2024， 45（1）： 103-111. [百度学术]

LAADIAL K， SAHRAOUI M， CARDOSO A J M. On-line Fault Diagnosis of DC-link Electrolytic Capacitors in Boost Converters Using the STFT Technique［J］. IEEE Transactions on Power Electronics， 2021， 36（6）： 6303-6312. [百度学术]

MAQSOOD A， OSLEBO D， CORZINE K， et al. STFT Cluster Analysis for DC Pulsed Load Monitoring and Fault Detection on Naval Shipboard Power Systems［J］. IEEE Transactions on Transportation Electrification， 2020， 6（2）： 821-831. [百度学术]

陈维兴，崔朝臣，李小菁，等. 基于多种小波变换的一维卷积循环神经网络的风电机组轴承故障诊断［J］. 计量学报， 2021， 42（5）： 615-622. [百度学术]

CHEN W X， CUI Z C， LI X J， et al. Bearing Fault Diagnosis of Wind Turbine Based on Multi-wavelet-1 D Convolutional LSTM［J］. Acta Metrologica Sinica， 2021， 42（5）： 615-622. [百度学术]

吴建章，梅飞，郑建勇，等. 基于改进经验小波变换和 XGBoost 的电能质量复合扰动分类［J］. 电工技术学报， 2022， 37（1）： 232-243，253. [百度学术]

WU J Z， MEI F， ZHENG J Y， et al. Recognition of Multiple Power Quality Disturbances Based on Modified Empirical Wavelet Transform and XGBoost［J］. Transactions of China Electrotechnical Society， 2022， 37（1）： 232-243，253. [百度学术]

KHOKHAR S， ZIN M A A， MEMON A P， et al. A New Optimal Feature Selection Algorithm for Classification of Power Quality Disturbances Using Discrete Wavelet Transform and Probabilistic Neural Network［J］. Measurement， 2017， 95： 246-259. [百度学术]

THIRUMALA K， PRASAD M S， JAIN T， et al. Tunable-Q Wavelet Transform and Dual Multiclass SVM for Online Automatic Detection of Power Quality Disturbances［J］. IEEE Transactions on Smart Grid， 2018， 9（4）： 3018-3028. [百度学术]

金海龙，邬霞，樊凤杰，等. 基于GST-ECNN的运动想象脑电信号识别方法［J］. 计量学报， 2022， 43（10）： 1341-1347. [百度学术]

JIN H L， WU X， FAN F J， et al. Motor Imagery EEG Signal Recognition Method Based on GST-ECNN［J］. Acta Metrologica inica， 2022， 43（10）： 1341-1347. [百度学术]

CUI C H， DUAN Y J， HU H L， et al. Detection and Classification of Multiple Power Quality Disturbances Using Stockwell Transform and Deep Learning［J］. IEEE Transactions on Instrumentation and Measurement， 2022， 71： 1-12. [百度学术]

VENKATESWARA REDDY M， SODHI R. A Modified S-transform and Random Forests-based Power Quality Assessment Framework［J］. IEEE Transactions on Instrumentation and Measurement， 2018， 67（1）： 78-89. [百度学术]

许立武，李开成，罗奕，等. 基于不完全 S 变换与梯度提升树的电能质量复合扰动识别［J］. 电力系统保护与控制， 2019， 47（6）： 24-31. [百度学术]

XU L W， LI K C， LUO Y， et al. Classification of Complex Power Quality Disturbances Dased on Incomplete S-transform and Gradient Boosting Decision Tree［J］. Power System Protection and Control， 2019， 47（6）： 24-31. [百度学术]

LIANG C B， TENG Z S， LI J M， et al. Improved S-transform for Time-Frequency Analysis for Power Quality Disturbances［J］. IEEE Transactions on Power Delivery， 2022， 37（4）： 2942-2952. [百度学术]

滕召胜，王永，李建闽，等. 一种新的谐波时频分解方法—K-S分解［J］. 中国科学（技术科学）， 2019， 49（2）： 234-242. [百度学术]

TENG Z S， WANG Y， LI J M， et al. A New Method of Harmonic Time-Frequency Decomposition： The K-S Decomposition［J］. Scientia Sinica （Technologica）， 2019， 49（2）： 234-242. [百度学术]

基于优化窗函数改进S变换的低频振荡暂态检测方法

摘要

关键词

1 引 言

2 改进S变换算法

2.1 ST原理

2.2 改进S变换算法

3 算法快速实现

3.1 MST的Fourier变换表达形式

3.2 离散MST

3.3 MST快速实现方法