使用Chrome浏览器效果最佳，继续浏览，你可能不会看到最佳的展示效果，

确定继续浏览么?

复制成功，请在其他浏览器进行阅读

精密角位置信号数字化测量系统的研究

- ORCID：
游立 ^1,2
✉
- ORCID：
王书强 ²
- ORCID：
金海彬 ²
- ORCID：
李亚琭 ²
✉
- ORCID：
关振宇 ¹

1. 北京航空航天大学网络空间安全学院，北京 100191； 2. 北京东方计量测试研究所计量事业部，北京 100086

中图分类号： TB922； TB97

最近更新：2025-02-06

DOI： 10.3969/j.issn.1000-1158.2025.01.19

摘要

感应同步器、旋转变压器是一类基于电磁感应原理的角位置传感器，广泛应用于自动控制、伺服系统中，其输出信号是一组随角位置变化呈比例关系的交流电压信号。要对该信号实现精密测量或校准需要使用专用角度指示器，此仪器功能单一且价格高昂。因此，使用通用数字化仪研制了一套精密角位置信号数字化测量系统，实现了分辨力达0.000 1°，测量准确度达±0.001°（k=2）的同步分解信号测量能力。该系统不仅可应用于角度模拟器、感应同步器、旋转变压器的校准或检测中，相关技术还可以应用于国产化精密角度指示器研制中，具有良好的应用前景。

关键词

角位置测量; 角度指示器; 采样技术; 旋转变压器; 感应同步器

1 引言

感应同步器和旋转变压器是一类基于电磁感应原理的角位置传感器^［

1］，其输出信号是一组随角位置变化呈比例关系的交流电压信号，也被称为同步分解信号，具有可靠性高，环境适应性好等优点，应用在新能源汽车驱动、控制力矩陀螺、伺服系统等自动控制装置中^{［参考文献 2~9}2~9］。这类角位置传感器与旋转变压器数字转换器（resolver digital converter，RDC）、感应同步器数字转换器（synchro digital converter，SDC）等一同组成角度测量装置^{［参考文献 10

百度学术}10］。在计量测试工作中，往往还使用了精密角度模拟器来校准感应同步器和旋转变压器配套角度变换器，如美国北大西洋工业公司的5330A^{［参考文献 11

百度学术}11］，其静态角度分辨力达0.001°，准确度达±0.003°。此类设备的校准问题同样值得关注，通常可以采用商业化精密角度位置指示器来实现，如美国北大西洋工业公司的8810AH^{［参考文献 12

百度学术}12］，其具备0.000 1°测量分辨力和±0.001 5°的测量准确度，但是其测量准确度不够高，引入的测量不确定度大于5330A的1/3，且价格高昂，功能相对单一，对计量实验室而言购置、使用和维护成本较高。

另一种校准精密角度模拟器的方法是采用感应比例法，如同步分解电桥^［

13］或感应比例电桥^{［参考文献 14

百度学术}14］，测量不确定度达0.000 6°（k=2），准确度高。但是存在频率范围窄、设备复杂、操作繁琐等不足，不便于基层计量实验室及现场作业应用。

为满足高效计量效率及保证量值传递准确度的需要，最优办法是设计一台静态角度测量准确度达±0.001°，分辨力达0.000 1°水平的精密角位置信号测量系统。根据对同步分解信号的特征分析，可以用采样测量法通过测量交流电压信号基波幅值的比例关系实现角位置测量功能。用这种方法，要求采样装置具有良好的动态范围、信噪比和线性度。因此，我们使用了高性能数字化仪NI PXI-5922^［

15］，参考相关技术指标的测试数据^{［参考文献 16

百度学术}16］，开发了角度测量验证软件，实现了精密静态角位置测量功能。

为减小同步分解信号畸变、干扰等非正弦信号的影响，并减小由于采样频率泄漏带来的测量误差，在测量软件的开发中采用了三谱线频率估计法^［

17］测量基波频率，应用相敏检波技术^{［参考文献 18

百度学术}18］实现基波幅值比例的精密测量功能。在完成测量软件开发后，利用更精密的角度模拟器对研制的精密角位置信号测量系统进行测试，结果表明其分辨力和准确度均满足需求。这种方法在静态角位置测量中具有良好的效果。

2 测量原理

2.1　信号特征

旋转变压器或感应同步器的输出同步分解电信号，是转子与定子间根据空间轴角相对位置，通过加载在定子上得励磁电压信号，在转子上感应输出的一组与空间角度信号相关的电信号。其中，分解信号一组两相四线组合的同频同相正弦电压信号，其转子绕组空间夹角呈90°关系，同步信号是一种三相三线组合的同频同相正弦信号，转子绕组空间夹角为120°，如图1所示^［

19］。

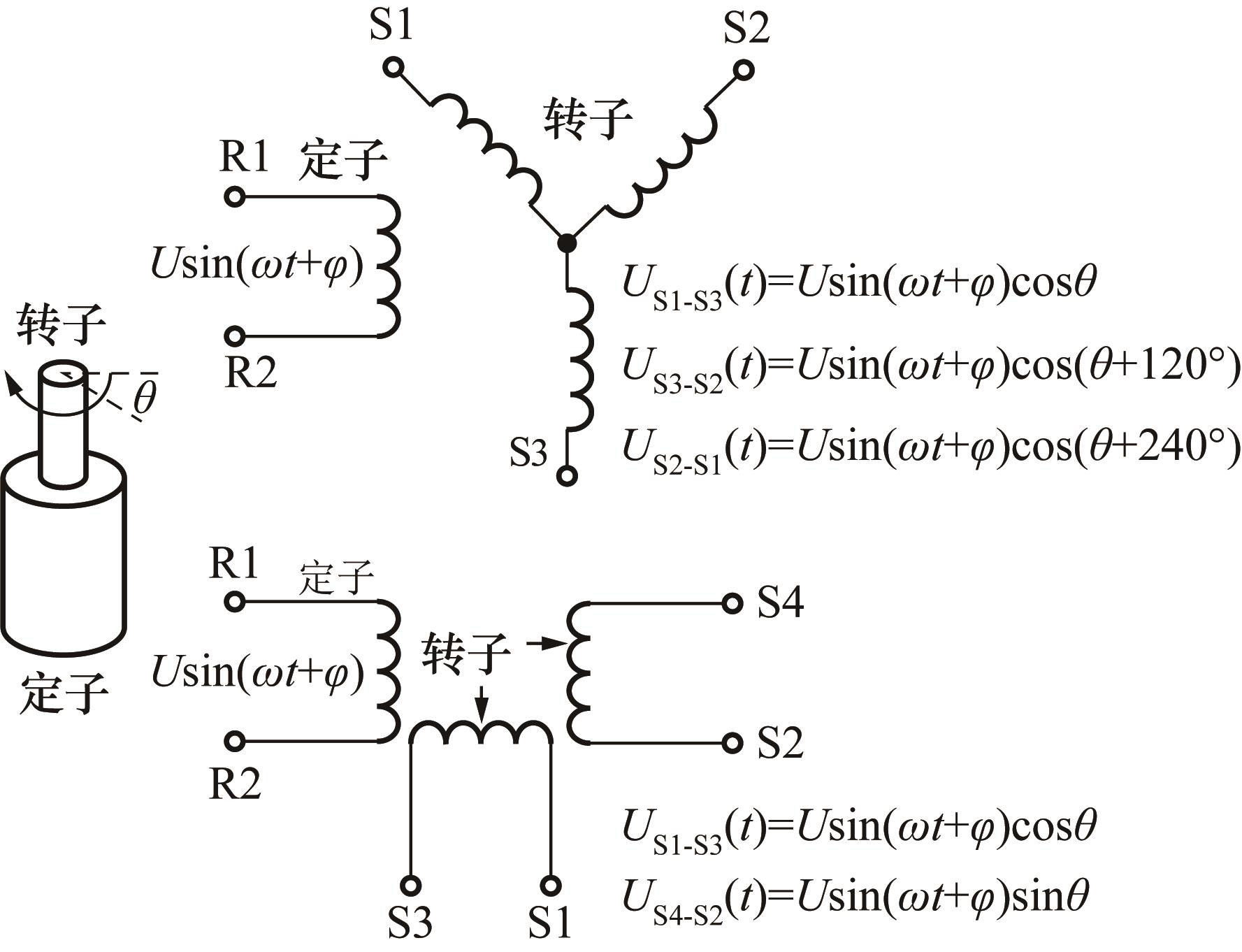
图1 感应同步器和旋转变压器的测量原理及输出信号

Fig.1 Measurement principle and output signal of synchro and resolver

在感应同步器或旋转变压器工作时，激励信号被加载在定子绕组上。激励信号一般频率为50 Hz~20 kHz的正弦或方波信号，一些新型角度传感器工作频率甚至可达100 kHz。激励信号通过电磁感应效应，被耦合至转子绕组上，输出相应的同步或分解信号。根据图1中的式子，同步分解电信号的幅值比通过三角函数变换，可以解算转子与定子间偏转几何轴角量θ。在感应同步器上，任何一对转子输出端电压是另2个端电压的矢量和。

感应同步器或旋转变压器还具备角速度测量功能。当测量恒定的角速度时，旋转变压器输出的信号如图2所示。其正弦分量和余弦分量近似调幅信号，包络信号的角频率与角速率成恒定的比例关系。

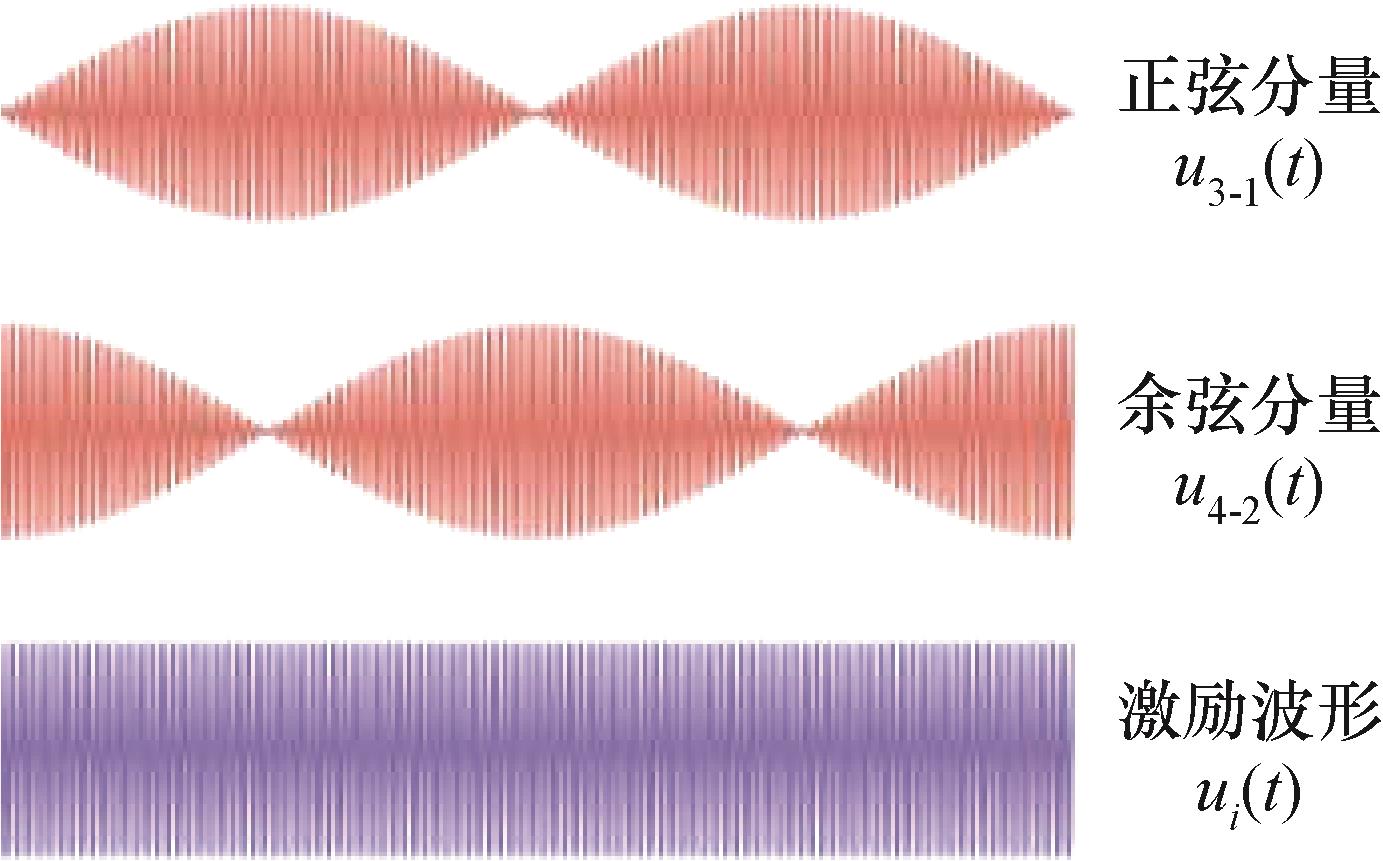
图2 旋转变压器输出动态角位置信号波形示意图

Fig.2 The output dynamic signal waveform of resolver

相比于感应同步器，旋转变压器的结构更为紧凑，价格更便宜，被广泛应用于民用工业及国防装备中。大多数旋转变压器工作在2 ~40 V下，频率400 Hz~10 kHz，测角准确度在0.008°~0.08°之间。为满足更高的测角分辨力和精度需求，设计有多个转子绕组的双极性旋转变压器具有更高的性能。

2.2　测量方法

根据同步分解的信号特征，角位置测量精度取决于转子输出的信号幅值比例测量精度。以分解信号为例分析，理想正弦通道、余弦通道输出信号的时域表达式为：

\{\begin{array}{l} u_{3 - 1} (t) = U s i n (ω t + φ) s i n θ \\ u_{2 - 4} (t) = U s i n (ω t + φ) c o s θ \end{array}

（1）

式中： $u_{3 - 1} (t)$ 是正弦通道输出信号； $u_{2 - 4} (t)$ 是余弦通道输出信号；U是转子耦合的最大电压幅值；ω是励磁信号的角频率； $θ$ 是转子与定子的相对角位置值；φ是正余弦通道与励磁信号之间的相位差。那么将 $u_{3 - 1} (t)$ 和 $u_{2 - 4} (t)$ 相除，从而得：

k = \frac{u_{3 - 1} (t)}{u_{2 - 4} (t)} = \frac{U_{3 - 1}}{U_{2 - 4}} = \frac{s i n θ}{c o s θ} = t a n θ

（2）

式中：k为 $u_{3 - 1} (t)$ 和 $u_{2 - 4} (t)$ 的幅值比； $U_{3 - 1}$ 是正弦通道输出信号的幅值； $U_{2 - 4}$ 是余弦通道输出信号的幅值。通过测量 $u_{3 - 1} (t)$ 和 $u_{2 - 4} (t)$ 幅值比，和反正切计算，能够得到角位置值 $θ$ 的计算函数为：

θ = a r c t a n k = a r c t a n \frac{U_{3 - 1}}{U_{2 - 4}}

（3）

由于正切函数在 $(1 / 2) π$ 、 $(3 / 2) π$ 位置有垂直渐进线，因此要避免 $U_{2 - 4}$ 接近于0的情况。

不仅如此，在测量过程中还应该尽量避免式（3）中，k远大于1的情况。根据测量不确定传播律^［

20］，将引起测量不确定度的增长，因此在k＞1时，可采用反余切计算角位置值

θ

：

θ = a r c c o t \frac{1}{k} = a r c c o t \frac{U_{2 - 4}}{U_{3 - 1}}

（4）

然而，式（3）和式（4）都是建立在角位置在第一象限条件下计算，仅通过式（3）和式（4）是无法判定角位置在0°~360°的哪个象限，因此还需要通过测量正弦通道、余弦通道的信号与激励信号之间的相位差关系，从而判定角位置的工作象限。其基本判定原则如表1所示。

表1 正弦通道、余弦通道信号与激励信号相位关系与较为象限对应表

Tab. 1 Relationship between Angular Position Quadrant to Phase of Sine/Cosine Signals to Excitation Signal

与激励信号的相位关系	正弦通道	余弦通道	角位置象限
	同相	同相	1
	反相	反相	3
	同相	反相	4
	反相	同相	2

通过反正切/余切计算和象限判定2个步骤，实现了电压比例和相位关系到角位置值的计算过程。类似的，可以通过四线-三线电压的换算关系，计算同步信号的角位置值。

3 测量系统设计

根据测量原理，可以设计一个精密角位置信号数字化测量系统，如图3所示。采用A/D变换装置，对旋变角位置信号的正弦通道和余弦通道的电压进行量化，再通过数字信号处理单元测量 $U_{3 - 1}$ 和 $U_{2 - 4}$ 的大小或比例。同时，通过A/D变换装置和数字信号处理单元，分别测量 $u_{3 - 1} (t)$ 和 $u_{2 - 4} (t)$ 与激励信号 $u_{i} (t)$ 的相位关系φ。最后，通过反正切/余切计算和相位关系与象限判定表，从而求解出角位置值。

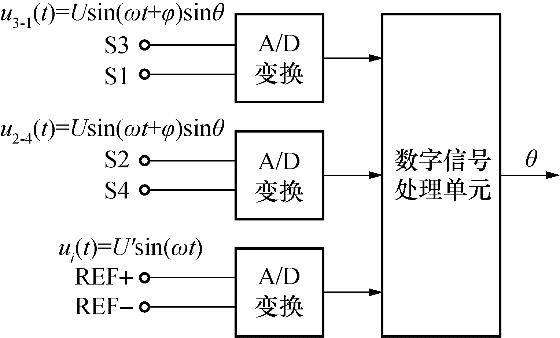
图3 精密角位置信号数字化测量系统的原理图

Fig.3 Schematic diagram of precision angle position signal digital measurement system

3.1　硬件配置

为了保证角位置测量准确度达±0.001°，测量分辨力达0.000 1°，A/D变换装置测量信号幅值应该具有足够的线性度和分辨能力。对式（3）求导，得：

d θ = \frac{1}{1 + k^{2}} d k \leq d k

（5）

角度测量准确度±0.001°，对应的弧度值为1.7×10^-5 rad，由（4）式可知电压比测量准确度至少应达到±1.7×10^-5，分辨力应达到1.7×10^-6。对应的A/D变换的分辨力应不少于20位，交流电压测量的非线性误差小于1.7×10^-5。因此，可以使用高分辨率、高速和高线性数字化仪或采样数字万用表实现角位置信号测量。

基于这样的要求，选用了2块NI PXI-5922数字化仪卡实现A/D变换功能，每块卡都有2个采样通道，有2 V和10 V这2个量程，具有24位分辨力，积分非线性优于-100 dB，无杂散动态范围（SFDR）优于120 dBFs（10 kHz下），采样率为50 kS/s ~ 15 MS/s，非常适用于角位置信号测量系统的应用需求。因此基于图3所示测量原理设计的组成如图4。

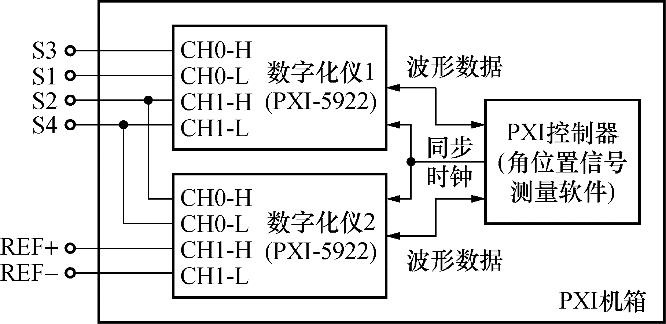
图4 精密角位置信号数字化测量系统的组成图

Fig.4 Composition diagram of precision angle position signal digital measurement system

精密角位置信号数字化测量系统中，2块数字化仪卡实现了3个通道的A/D变换功能。PXI控制器实现数字信号处理单元的功能，通过PXI总线实现波形数据交互、同步时钟以及同步触发功能。PXI机箱则将测量系统集成在一个机箱内。

3.2　测量算法与软件

根据精密角位置信号数字化测量系统的工作原理，A/D变换将正余弦通道信号、励磁信号量化后，是3个长数组，同时这个信号还混叠了其他频率的噪声信号，而根据式（1） ~ 式（4）的表述，应当解算出激励信号同频的正弦通道和余弦通道信号的幅值比。基于这样的测量需求，相敏检波测量算法具有优势。

相敏检波算法提取频率幅值信号的前提是需要精确的测量被测信号的基波频率，同时还应当尽可能的减小非整周期采样带来的频谱泄漏问题，因此设计计算步骤如下：

1）测量励磁信号的基波频率f₀；

2）根据采样率f_s，采样点数L，基波频率f₀，求解L下最大整周期点数L′；

3）将正余弦信号的采样点数截取至L′；

4）根据f₀和f_s比值，构建一组正交基，分别与截断后正余弦信号相乘、平均，求解正余弦信号幅值比、相位差；

5）采用和4）相同的方法，求解余弦通道和正弦通道的相位差；

6）根据幅值比进行反正切/反余切计算，根据相位差关系，求解角位置值。

根据上述6个测量步骤，可以设计一套基于相敏检波原理的角位置信号测量算法，实现角位置信号测量功能，并可以减小信号畸变、非整周期带来的测量误差，提高角位置测量准确度和分辨力，满足计量校准的需要。

角位置信号测量算法的具体实现步骤如下：

1）将 PXI-5922数字化仪卡的采样率f_s设置为100kS/s，每个通道的采样存储深度L设置为100 000点，对励磁信号、正余弦信号采样，测量结果传输至PXI控制器；

2）处理励磁信号采样数据，进行FFT变换，此时频率分辨力为1 Hz，找出最大谱线F_k，提取相邻谱线F_k_-1和F_k₊₁，计算基波频率为：

f_{0} = (k + δ) \frac{f_{s}}{L}

（6）

δ = - R e (\frac{F_{k + 1} - F_{k - 1}}{2 F_{k} - F_{k + 1} - F_{k - 1}})

（7）

根据f₀和f_s，按公式（7）计算求解L=100kpts下最大整周期点数L′，

L^{'} = ⌊\frac{L f_{0}}{f_{s}}⌋

（8）

3）根据f₀和f_s，构建一组数字正交基a［n］和b［n］，进行相敏检波计算，其中：

a [n] = s i n (\frac{2 n π f_{s}}{L f_{0}}), n = 0,1, 2, \dots, L^{'}

（9）

b [n] = c o s (\frac{2 n π f_{s}}{L f_{0}}), n = 0,1, 2, \dots, L^{'}

（10）

正交基分别与截断后正余弦信号相乘、平均，求解正余弦信号幅值比、相位差，角位置值计算过程如图5所示，相位差计算式为：

φ = a r c c o s (- \frac{u_{1 x} u_{2 x} + u_{1 y} u_{2 y}}{\sqrt[]{u_{1 x}^{2} + u_{1 y}^{2}} \cdot \sqrt[]{u_{2 x}^{2} + u_{2 y}^{2}}})

（11）

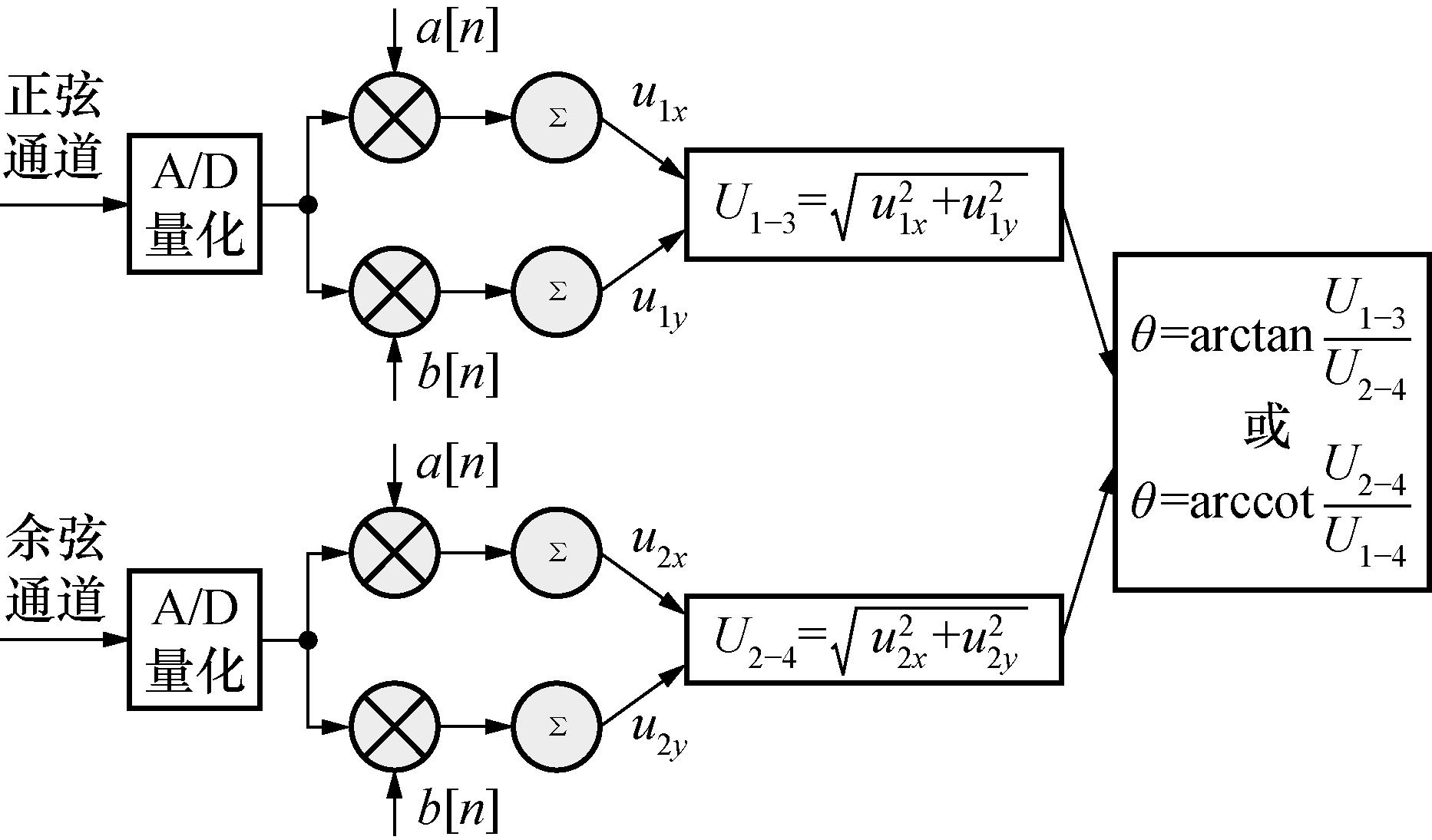
图5 基于相敏检波算法的角位置值计算过程

Fig.5 The calculation process of angle position signal results based on phase sensitive detection algorithm

4）类似的，用步骤3）方法，计算余弦通道 $u_{2 - 4} (t)$ 与激励信号 $u_{i} (t)$ 的相位关系，根据表1判据，判定角位置值的象限，并按照0°~360°或-180°~+180°的格式显示角位置值。

根据以上算法，基于NI LabVIEW平台开发了基于相敏检波算法的角度测量验证软件，具备角位置信号测量功能，可对角度模拟器的旋变/同步信号进行测量并得到角度值。

3.3　测试验证

角位置信号测量系统的性能采用精密角度模拟器NAI 5300用比较法进行验证，如图6所示。

图6 用NAI 5300角度模拟器验证试验

Fig.6 Verification by NAI5300 synchro resolver simulator

NAI 5300型精密角度模拟器的频率范围为47 Hz~20 kHz，线电压范围为1 V~90 V，分辨力为0.000 1°，最佳测量不确定度为0.000 6°（k=2）。将角度模拟器输出线电压设置为3.5V，数字化仪卡PXI-5922设为10 V量程，在47 Hz~20 kHz频率范围下选取若干测试频率，每个测试频率下，在0°~360°角度范围内均匀选取23个角度点进行验证测试，计算平均角度示值误差和该频率点下的误差分布范围，测量结果如图7所示。结果表明，角位置信号测量系统在5 kHz以下的角位置测量误差均小于±0.001°，15 kHz以下小于±0.001 5°，20 kHz以下小于±0.002°，具有良好的准确度。

图7 47 Hz~20 kHz频率范围下角位置测量系统的测量误差和分布

Fig.7 Measurement error and deviation of angle position measurement system from 47 Hz to 20 kHz

此外，受限于精密角度模拟器的性能，角度分辨力尚未有较为规范的验证方法，采用了一种简易的验证方法。具体步骤如下：

1）将角度模拟器频率设置1 kHz点下，角度值设置为30.000 0°，读取角位置测量系统测量起始值；

2）将角度模拟器按0.000 1°步进增加角度值，每个角度值下用角度指示器测量10个点，取平均值减去起始值作为增量值，共选取10个增量点，角度模拟器设置值停止于30.001 0°；

3）比较每个增量值与累计步进值的差值，当差值的最大值小于0.000 15°时，认为角度测量分辨力达到了0.000 1°。角度分辨力的测量结果如图8所示，由于示值增量的平均值与角度增量的一致性好明显小于0.000 1°，因此可以认为分辨力达到0.000 1°的性能水平。

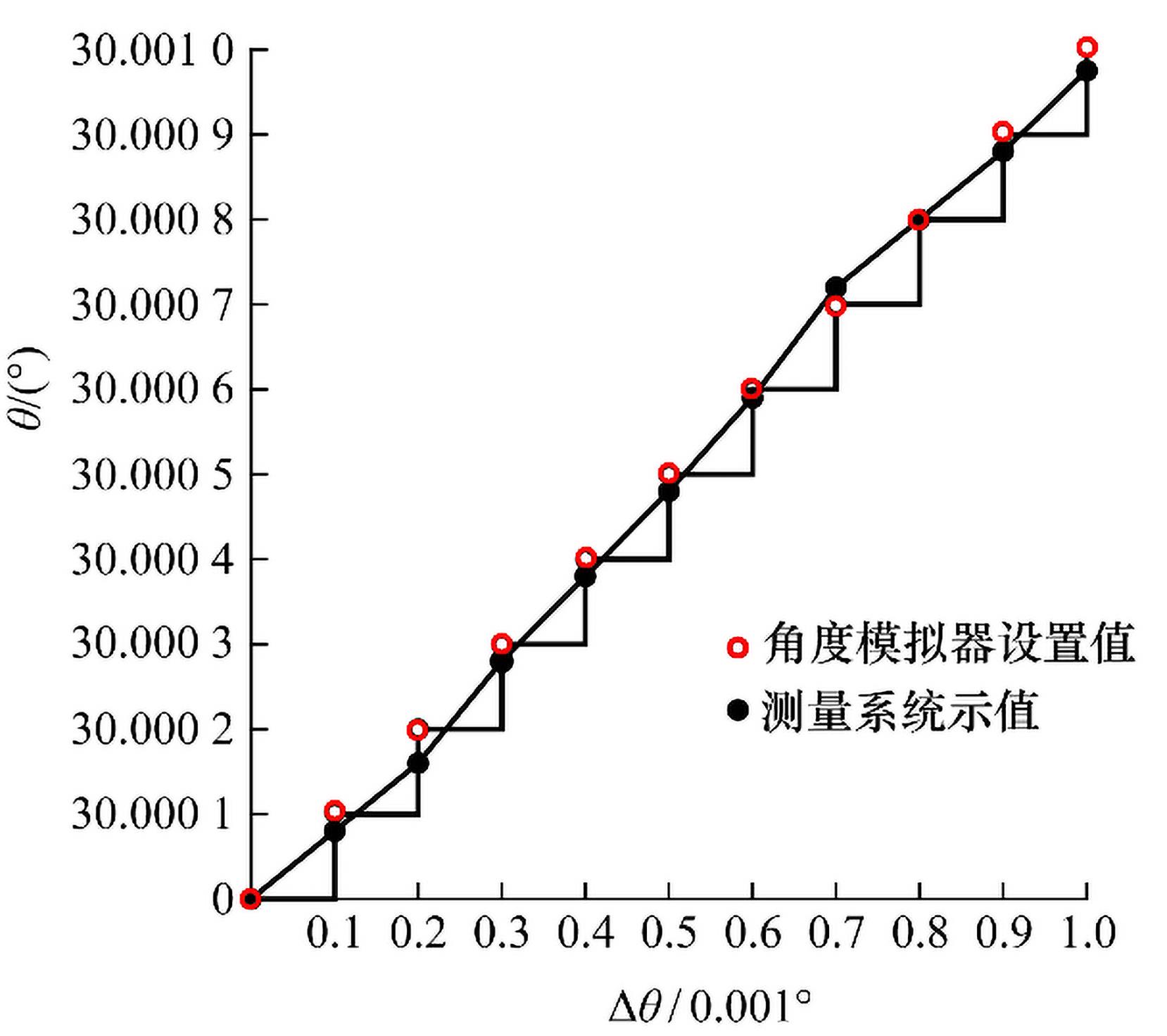
图8 测量系统在1 kHz下30°附近的分辨力测试结果

Fig.8 Diagram of the resolution test results of measurement system near 30°at 1 kHz

4 测量不确定度评估

根据第3.3节所述的比较法，精密角位置数字化测量系统的示值误差可以用下式描述：

Δ θ = θ_{r} - θ_{s}

（12）

式中： $Δ θ$ 是角位置示值误差； $θ_{r}$ 是角位置示值； $θ_{s}$ 是角位置标准值。

因各输入量不相关，示值误差的标准测量不确定度传播可用式（12）表示。

u_{c} (Δ θ) = \sqrt[]{c^{2} (θ_{r}) u^{2} (θ_{r}) + c^{2} (θ_{s}) u^{2} (θ_{s})}

（13）

式中：灵敏系数为 $c (θ_{r}) = 1$ ； $c (θ_{s}) = - 1$ 。

对于 $u (θ_{r})$ ，根据式（1）描述的旋转变压器的角位置信号特征和精密角位置数字化测量系统的测量原理。在开始测量时，正余弦通道加载同一个正弦电压信号，从而产生一个绝对的45°的角位置信号，通过每次测量前，进行软件自校准的操作可以修正采样通道间增益漂移带来的误差。因此，采样通道的增益漂移并不会贡献测量不确定度。

在此条件下，精密角位置数字化测量系统的测量不确定度来源主要来自采样通道间的非线性引起的示值误差 $u_{l i n e a r} (θ_{r})$ 和随机误差 $u_{r a n d o m} (θ_{r})$ 。

$u_{l i n e a r} (θ_{r})$ 在不同频率下表征为不同角度下的示值误差分布，即图7所示。 $u_{r a n d o m} (θ_{r})$ 是随机噪声、热噪声带来的重复性误差，可以通过贝塞尔公式计算，但通过测试发现，示值变化小于0.000 1°，可以忽略。

下面以在1 kHz点为例分析精密角位置数字化测量系统的测量不确定度，其中示值误差分布最大偏差为0.000 7°，由此引入的不确定度按B类评定。设为均匀分布，包含因子 $k = 2 \sqrt[]{3}$ ，那么由于由于示值误差限引入的测量不确定度为：

u (θ_{r}) = \frac{0.000 7 °}{2 \sqrt[]{3}} = 0.000 2 °

（14）

$u (θ_{s})$ 是NAI 5300型角度模拟器作为标准器，带来的测量不确定度。根据NAI 5300手册给出的测量不确定度为0.000 6°，包含因子k=2，那么有：

u (θ_{s}) = \frac{0.000 6 °}{2} = 0.000 3 °

（15）

将式（14）、（15）代入式（13），可计算示值误差标准不确定度为：

u_{c} (Δ θ) = \sqrt[]{0.000 2^{2} + 0.000 3^{2}} = 0.000 4 °

（16）

测量结果近似正态分布，取k=2，p=95%，有：

u (Δ θ) = k u_{c} (Δ θ) = 0.000 8 °

（17）

类似的，可以计算其他频率下测量不确定度。

5 结论

通过研制一套精密角位置信号数字化测量系统，验证了基于相敏检波算法的角位置信号测量方法，实现了分辨力达0.000 1°，测量准确度达±0.001°的角位置信号测量能力。然后，基于上述原理设计精密角位置信号数字化测量系统，可以应用于准确度达±0.003°的角度模拟器计量校准或旋转变压器、感应同步器的测试工作。但是，由于本装置研制过程重点在于方法的验证，电压测量范围须根据实际需要配备经校准的交流分压器，以满足相应的计量测试需要。

参考文献

KONX L. Synchro and Resolver Performance Definitions［J］. IRE Transactions on Component Parts， 1956， 3（3）： 88-98. [百度学术]

洪陆英. 新能源汽车永磁同步电动机控制系统故障维修［J］. 内燃机与配件， 2024（10）：70-72. [百度学术]

HONG L Y， The New Energy Automobile at the Same Timemotor Control Systematic Fault of Permanent Magnetism is Repaired［J］. Internal Combustion Engine & Parts， 2024（10）：70-72. [百度学术]

邵长胜，陈海鹏. 控制力矩陀螺速率控制中测角系统的研究［J］. 中国惯性技术学报， 2004，12（1）：77-80. [百度学术]

SHAO C P， CHEN H P. Angle Measuring System in SG-CMG Velocny Control［J］. Journal of Chinese Inertial Technology， 2004，12（1）： 77-80. [百度学术]

王林. 压力补偿式深海伺服电机及其角度传感器选型［J］. 现代制造技术与装备， 2024， 60（4）： 124-126. [百度学术]

WANG L， Pressure Compensation Deep-Sea Servo Motorand Its Angle Sensor Selection［J］. Modern Manufacturing Technology and Equipment， 2024， 60（4）： 124-126. [百度学术]

贾萍，胡博，宋力，等. 井下高温电机伺服控制器的设计与实现［J］. 工业控制计算机， 2023， 36（08）： 154-155. [百度学术]

JIA P， HU B， SONG L， et al. Design and Implementation of Downhole High Temperature Motor Servo Controller［J］. Industrial Control Computer， 2023， 36（08）： 154-155. [百度学术]

周会达. 基于RTLinux的高精度角位置信号测量系统设计与实现［J］. 电子测试， 2016（17）：4-5. [百度学术]

ZHOU H D， Design and implementation of high accuracy angular position measurement system based on RTLinux［J］. Electronic Test， 2016（17）： 4-5. [百度学术]

TIAN L， WU D， WEI D， HU Y， et al. Fault diagnose and tolerance technology for position detecting system based on dual resolvers［C］// Proceedings of 2014 IEEE Chinese Guidance， Navigation and Control Conference. Yantai， China， 2014： 529-533. [百度学术]

REN L， SUN S， XIAO C， et al. Research on fault diagnosis and position synthesize technology of resolver suitable for servo motor control［C］// CSAA/IET International Conference on Aircraft Utility Systems （AUS 2020）. Online Conference， 2020： 244-249. [百度学术]

LI H， CHEN X， LIU G， et al. A Disturbance Estimation Approach to Self-Calibration of Gimbal Resolver- to-Digital Conversion System［J］. IEEE Transactions on Industrial Electronics， 2023， 70（1）： 793-802. [百度学术]

XU N D. High Accuracy Resolver Simulator System with Fault Injection Function［J］. Analog Dialogue， 2019， 53（08）： 1-10. [百度学术]

North Atlantic Industries， 5330A Operations Manual - Includes Specifications ［EB/OL］. （2022-12-14）［2024-07-01］. https：//www.naii.com/ model/5330a. [百度学术]

North Atlantic Industries， 8810A Operations Manual （includes Specifications）［EB/OL］. （2019-02-28）［2024-07-01］. https：//www.naii.com/model/8810a. [百度学术]

Inc Tegam. MODEL DSRS-5DA DECADE SYNCO/RESOLVER STANDARD-Instruction ManualREV. A）［EB/OL］. （2014-06-01）［2024-07-01］. https：//tegam.com/wp-content/uploads/2015/10/DSRB-Manual-Rev-B.pdf. [百度学术]

金海彬，李小舟，王乾娟，等. 一种基于感应比例电桥平衡法的步分解标准器校准装置［J］. 计量学报，2021， 42（9）：1200-1205. [百度学术]

JIN H B， LI X Z， WANG Q J， et al， Induction Ratio Bridge Balance Method-based Synchro/Resolver Standard Calibration Device［J］， Acta Metrologica Sinica， 2021， 42（9）： 1200-1205. [百度学术]

Instruments National. SPECIFICATIONS PXI-5922 24-Bit， Flexible Resolution PXI Oscilloscope ［EB/OL］. （2018-09-26）［2024-07-01］. https：//download.ni.com/su-pport/manuals/374033b.pdf. [百度学术]

RIETVELD G， ZHAO D， KRAMER C， et al. Characterization of a Wideband Digitizer for Power Measurements up to 1 MHz［J］. IEEE Transactions on Instrumentation and Measurement， 2011， 60（7）： 2195-2201. [百度学术]

JACOBSEN E， KOOTSOOKOS P. Fast， Accurate Frequency Estimators ［DSP Tips & Tricks］［J］. IEEE Signal Processing Magazine， 2007， 24（3）： 123-125. [百度学术]

WU K， LI Y， LIU M. The implementation of the new type impedance measurement system［C］. 2014 XXXIth URSI General Assembly and Scientific Symposium （URSI GASS）， Beijing， China， 2014：1-4. [百度学术]

KESTER W， Resolver-to-Digital Converters-Analog Device Tutorial MT-030 ［EB/CD］.（2009-08-10）［2024-07-01］， https：//www.analog.com/2025-1-119/media/en/training -seminars/ tutorials/MT-030.pdf. [百度学术]

全国法制计量管理计量技术委员会. 测量不确定度评定与表示： JJF 1059.1-2012［S］. 北京：中国质检出版社，2012. [百度学术]

精密角位置信号数字化测量系统的研究

摘要

关键词

1 引 言

2 测量原理

2.1 信号特征

2.2 测量方法

3 测量系统设计

3.1 硬件配置

3.2 测量算法与软件

3.3 测试验证