能量天平水平安培力与电磁转矩引起对准能量误差的评估
1 引 言
近年来,质量量子基准研究已经成为国际计量领域研究的热点和难点。《Nature》杂志于2012年将质量量子计量基准研究列为目前世界6大科学难题之一。质量量子计量基准研究的主要内容,是通过实验将质量的单位千克溯源至普朗克常数h,实现单位千克基于基本物理常数的新定义。作为量子物理常数的普朗克常数,其只与微观粒子的状态和能级有关,拥有实物基准无法比拟的稳定性和准确性;一旦实现将质量的单位千克溯源至普朗克常数,则可借助普朗克常数的稳定性和准确性保证千克的稳定性和准确性[1]。
目前,国际上的质量量子计量基准研究方案主要分为两大类:第一类是通过微观的硅原子质量定义宏观的千克质量的阿伏伽德罗常数方案;第二类是利用机械功率(能量)和电学功率(能量)的等价性将质量单位千克溯源至普朗克常数的功率天平方案和能量天平方案[2~4]。其中,能量天平方案由中国计量科学研究院于2006年提出,该方案的核心部件由一个内置激励线圈的电磁体和一个悬挂线圈组成,其方法内涵是利用带电悬挂线圈在电磁体磁场内克服安培力做功量等于线圈电磁能量变化量的性质,将千克溯源至普朗克常数。在能量天平法实验测量结果中存在一项名为“对准误差”的主要误差分量。随着质量计量基准量子化研究逐步深入,在使用能量天平法将千克溯源至普朗克常数的方案中,电学量测量和机械装置设计等问题已得到基本确定,主要研究难点向特征矢量对准误差(alignment error)的测量补偿环节集中。
能量天平方案实验过程中,处于电磁体气隙内的通电线圈会受到安培力F和重力G的作用;而电磁体在运动装置驱动下将沿着竖直方向运动,如图1所示。其运动产生的位移量由激光干涉仪测得。线圈受到安培力F和重力G,线圈相对于电磁体的运动方向s,线圈位移测量激光束的方向λ,如图2所示。其中,线圈所受到的安培力F,线圈位移s以及测量激光束方向λ被用于表征线圈状态,因此3者被称为能量天平线圈的特征矢量。能量天平方案从原理上要求上述3种特征矢量均被对准于重力方向上,且各矢量作用点位于同一直线,否则普朗克常数的溯源结果将包含一项由该因素引起的系统误差,该系统误差被称为对准误差。
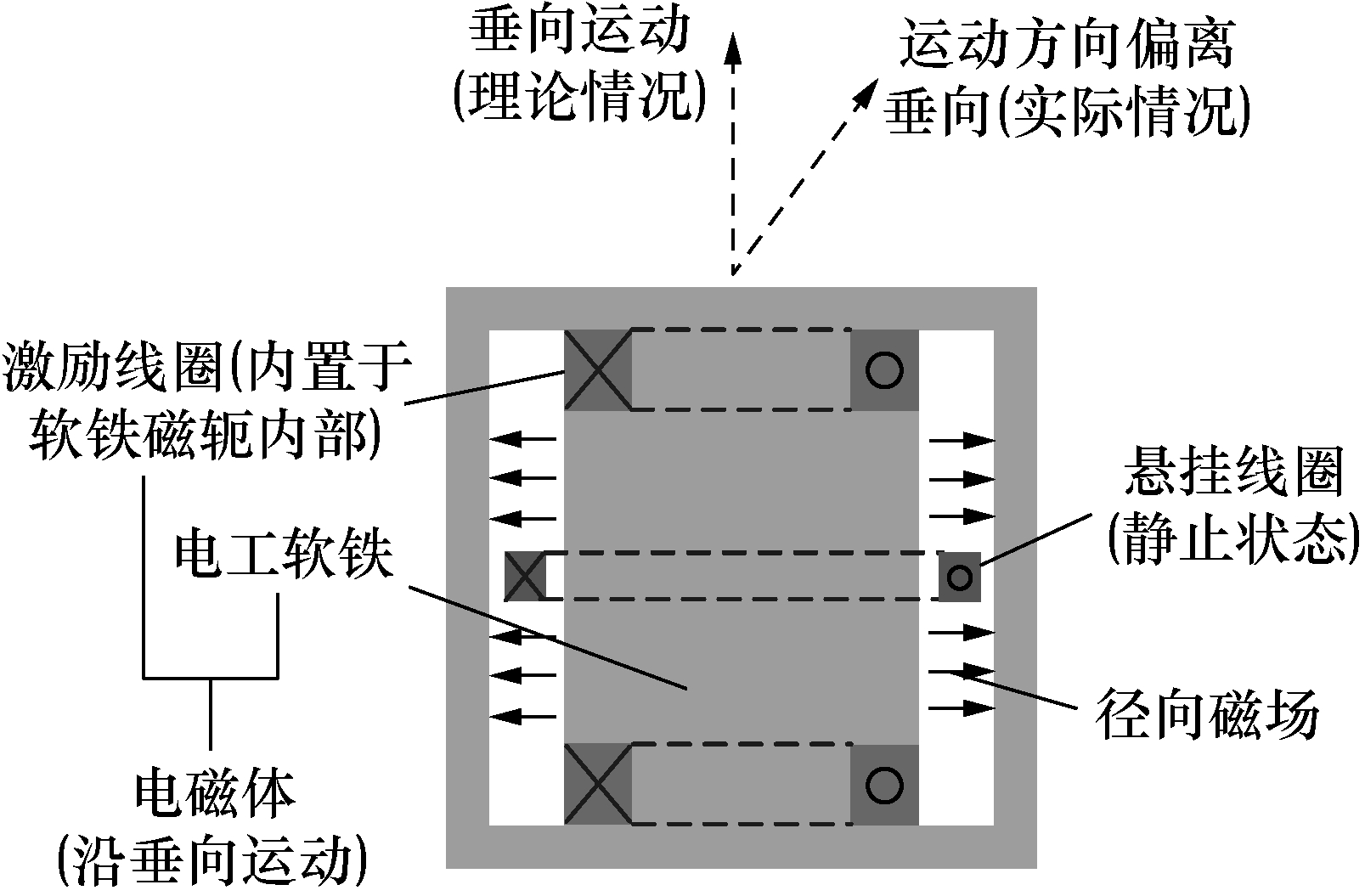
图1 能量天平实验装置中的悬挂线圈与电磁体

图2 能量天平特征矢量状态图
本文旨在针对目前能量天平方案中存在的主要系统误差——线圈对准误差,结合悬挂线圈机械结构建立水平安培力和电磁转矩的数学推导模型,设计了二维解耦机构对水平安培力和电磁转矩进行解耦,并采用电容传感器与激光干涉仪对电磁体的垂向运动进行监测,最终基于上述测量结果对能量天平对准误差进行评估。
2 能量天平原理简介
能量天平法原理如图3所示。在能量天平实验中,激励线圈组被内嵌于电工软铁磁轭内。当激励线圈内通过电流I2时,在软铁磁轭的气隙内将产生一径向磁场。悬挂线圈的位置正处于上述径向磁场内。悬挂线圈通以大小为I1的电流,则该悬挂线圈受到一垂向安培力Fz的作用,该安培力可表示为
Fz=(∂Φ/∂z)I1
(1)
式中:∂Φ/∂z是磁通量Φ在z方向上的梯度。当能量天平处于力平衡状态时,垂向安培力Fz与标准砝码的重力mg以及天平提供的平衡力Δfz(z)到达3力平衡状态:
(2)

图3 能量天平原理图
天平提供的平衡力Δfz(z)的大小可由精密质量比较器测得。
将式(2)左右两边取积分,积分路径从位置z1至z2;该积分过程在实际实验中由垂向位移平台驱动电磁体从z1运动至z2,而在此过程中悬挂线圈保持静止。如此由式(2)可得到
(3)
式(3)表明垂向安培力Fz从位置z1至z2做功量![]() 等于悬挂线圈与电磁体总电磁能量的变化量[Φ(z2)-Φ(z1)]I1,这也反映了该实验过程满足能量守恒定律。因此,基于原理式的千克定义方法被命名为能量天平法。
等于悬挂线圈与电磁体总电磁能量的变化量[Φ(z2)-Φ(z1)]I1,这也反映了该实验过程满足能量守恒定律。因此,基于原理式的千克定义方法被命名为能量天平法。
3 能量天平线圈对准误差
式(3)的成立要求能量天平的线圈各特征矢量满足下列条件:一是垂向安培力Fz与悬挂线圈重力G对准于同一方向上;二是电磁体相对于静止悬挂线圈的位移s与悬挂线圈重力G对准于同一方向上。但这两个对准条件在实际条件下难以完全满足。实际线圈的特征矢量对准状态如下:
能量天平方案实验包含两种实验模式:测力模式和测磁链差模式。测力模式实验过程大致可分为3步:首先,为悬挂线圈通以电流,产生作用于悬挂线圈的安培力;其次,利用垂向位移台驱动电磁体相对于静止悬挂线圈从位置z1运动至z2;最后,减小悬挂线圈中的电流直至电流等于零。
在上述测力模式过程中,若悬挂线圈中心平面与电磁体径向磁场不在同一平面内,如图4(a)所示,则作用于悬挂线圈的安培力将包含水平分量Fx(Fy)。另一方面,若悬挂线圈中心与径向磁场中心不在同一位置,如图4(b)所示,则将存在电磁转矩τy(τx)作用于悬挂线圈驱使线圈环绕水平反向运动。需要注意的是,图4的两个情况本质上体现的是悬挂线圈自身对应磁场与电磁体径向磁场轴线的重合程度,以及两条轴线与实验装置本地重力方向的重合程度。在实际实验和调试过程中,线圈轴线与线圈对应磁场轴线并不完全重合;因此,在调整线圈姿态以使线圈趋于对准状态的过程中,并不以线圈几何结构与电磁体横截面平行为目标,而是以线圈通电瞬间不受水平安培力作用而发生水平位移为目标。

图4 线圈特征矢量的两种非对准状态
电磁体相对于静止悬挂线圈的位移s在实际实验中不可能完全沿竖直方向,因为驱动电磁体运动的垂向位移平台方向无法完全调整至垂向,且位移平台的运动直线度也受到位移平台自身加工精度影响。
由于悬挂线圈受到水平方向安培力Fx(Fy)和电磁转矩τy(τx)的作用,悬挂线圈将发生沿水平方向的位移x(y)和绕水平方向的转动θy(θx),因此在实验过程中水平方向安培力Fx(Fy)和电磁转矩τy(τx)将对悬挂线圈做功,则原理式(3)变为如下形式
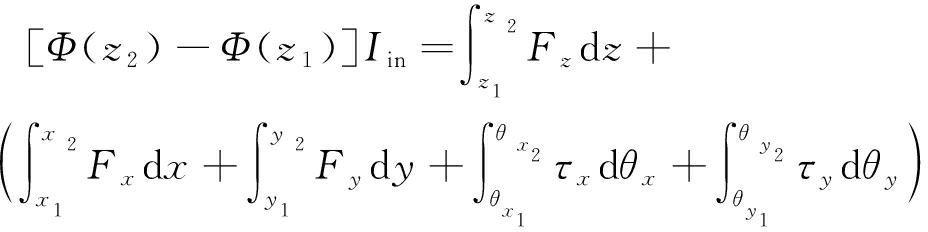
(4)
式(4)等号右边括号内的积分式之和即水平安培力和电磁转矩做的功,也就是对应的对准能量误差Wa
(5)
综上所述,能量天平线圈对准误差主要由线圈所受水平向安培力和电磁转矩对线圈做功引起;而线圈所受水平向安培力和电磁转矩之所以存在,其原因分别为线圈对应的磁平面与电磁体产生径向磁场的不平行和不同心。这里的不平行和不同心分别由特征矢量中的安培力F与线圈重力G方向不平行、安培力F与线圈重力G的作用点不在同一直线上所引起。另一方面,除线圈所受水平向安培力和电磁转矩之外,线圈在实验过程中发生的水平位移和环绕线圈自身水平轴的转动,也是水平向安培力和电磁转矩对线圈做功的必要因素。而线圈水平位移和环绕线圈自身水平轴的转动则受电磁体垂向位移平台的调整精度的影响;这部分影响,可归结为线圈运动矢量s偏离线圈重力G的方向所引起。
4 水平安培力与电磁转矩求解方法
为了消除式中的能量天平对准误差,首先需要分别求解水平安培力Fx(Fy)和电磁转矩τy(τx)的大小,其求解过程可分为“解耦力与力矩”,“力与力矩分别建模”,“测量力与力矩”和“测量水平位移与转角”等4部分。
4.1水平安培力与电磁转矩的解耦
能量天平过去采用传统的刀口结构作为承重主梁和线圈悬挂部分的过渡机构,悬挂部分最低位置连接着悬挂线圈。如前文所述,悬挂线圈在实际实验过程中将受到水平安培力和电磁转矩的作用。由于线圈上端连接着刀口结构,上述两种力学作用对线圈的作用效果均为驱使线圈以及其悬挂装置绕刀口支点位置摆动;若对力和力矩的作用效果进行测量则无法分别获取力与力矩的对应量值。
为解耦力与力矩,进而分别求解其对应量值,设计了双柔性铰链解耦机构,如图5所示。该解耦机构由上铰链、连接杆和下铰链构成,其中上铰链与下铰链均为二维不锈钢柔性铰链。整套线圈悬挂结构被上下铰链分隔为3个部分:OA(从质量比较器悬挂点O至上铰链位置A),AB(从上铰链位置A至下铰链位置B),BD(从下铰链位置B至悬挂线圈质心位置D)。AB段的质心位于位置E,其对应重力为mAg;BD段和线圈本身的等效质心位于位置C,其对应重力为mB。根据受力平衡原理对图5线圈悬挂结构的受力情况进行分析可知,由于下铰链(位置B)的存在,产生于线圈(位置D)的电磁转矩(τy,τx)无法通过位置B对位置A的上铰链产生影响,即转矩作用效果被下铰链阻挡于位置B以下,无法作用于AB段;而另一方面,同样产生于线圈(位置D)的水平安培力(Fx,Fy)则可以通过下铰链而对AB段产生力的作用。由上述内容可知,双柔性铰链机构分离了电磁转矩和水平安培力的有效作用区域,从而分离两者的作用效果,为两者独立求解模型的建立奠定基础。
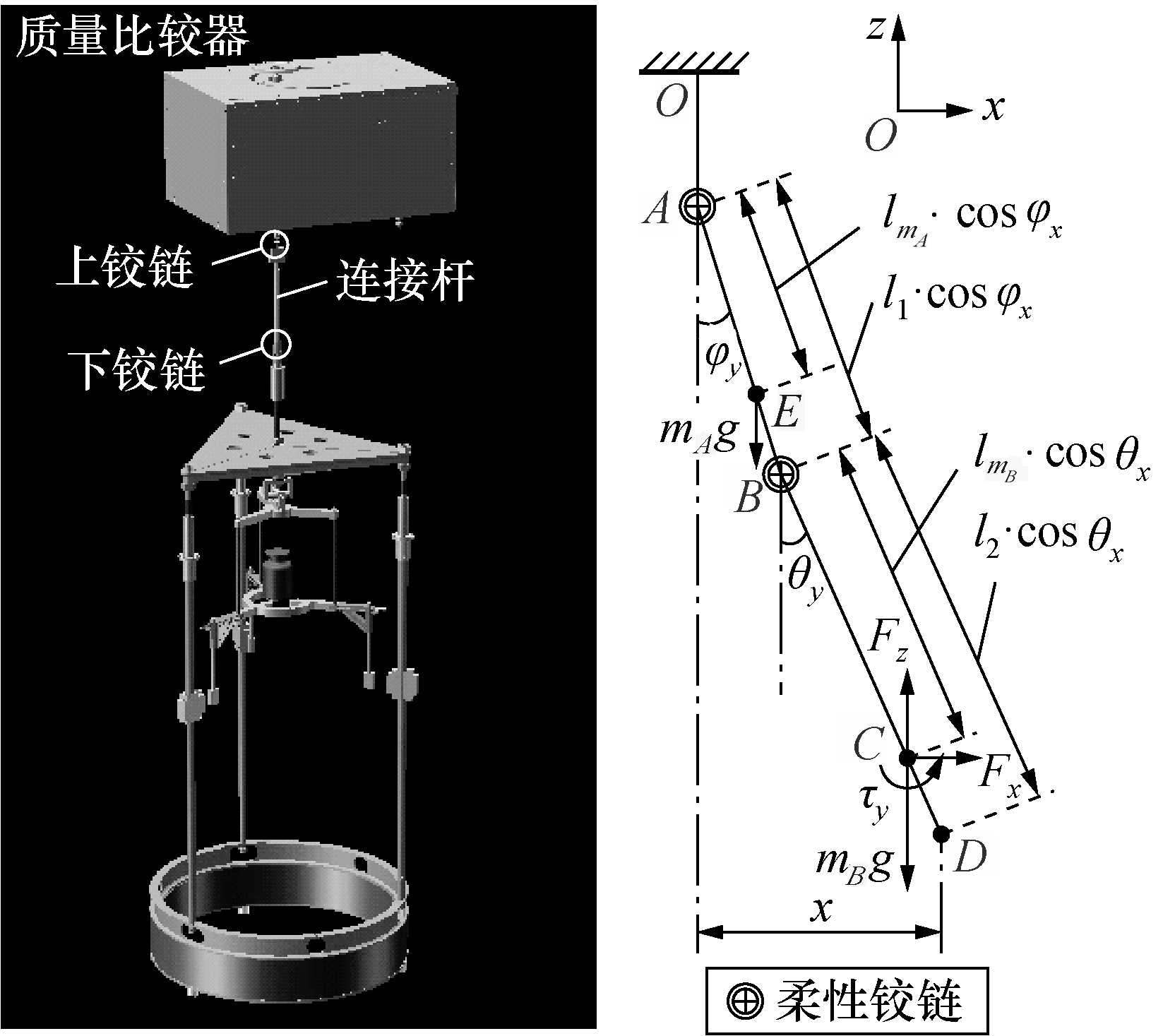
图5 线圈悬挂结构受力分析
4.2水平安培力与电磁转矩求解模型
为评估水平安培力与电磁转矩造成的对准误差,基于受力平衡原理对水平安培力与电磁转矩进行建模。如图5所示,在平面xOz内,处于电磁体径向磁场中的悬挂线一旦通电,则线圈将受到来自径向磁场的垂向安培力Fz,水平安培力Fx和电磁转矩τy的作用。在上述3种力学矢量的作用下,悬挂线圈的姿态将发生改变,由于双柔性铰链结构的存在,线圈姿态的改变量将体现于上下柔性铰链的角度改变量上。在垂向安培力Fz,水平安培力Fx,电磁转矩τy和线圈悬挂机构重力的共同作用下,线圈上电之后将重新达到受力平衡状态。不妨设假设平衡状态时,上柔性铰链在平面xOz内的角度改变量为φy,在平面yOz内的角度改变量为φx;下柔性铰链在平面xOz内角度改变量为θy,,在平面yOz内的角度改变量为θx。对于上铰链位置A可列写力矩平衡方程:
[(mAg·lmA+mBg·l1-Fz·l1)·sinφy-
Fx·cosφy·l1]·cosφx=0
(6)
[(mAg·lmA+mBg·l1-Fz·l1)·sinφx-
Fx·cosφx·l1]·cosφy=0
(7)
式中:lmA,l1分别为AE段和AB段的长度,因此AE段和AB段的长度在平面xOz内的投影长度为lmA·cosφy和l1·cosφy。
对于下铰链位置B也可列写力矩平衡方程:
[(mBg-Fz)·sinθy·lmB-
Fx·cosθy·lmB]·cosθx-τy=0
(8)
[(mBg-Fz)·sinθx·lmB-
Fy·cosθx·lmB]·cosθy-τx=0
(9)
式中:lmB和l2分别为BC段和BD段的长度。
根据式(6)~式(9)可分别推导出水平安培力与电磁转矩的表达式:
(10)
(11)
τy=[(mBg-Fz)·sinθy·lmB-
Fx·cosθy·lmB]·cosθx
(12)
τx=[(mBg-Fz)·sinθx·lmB-
Fy·cosθx·lmB]·cosθy
(13)
观察式(10)~式(13)可发现,Fx与Fy的表达式结构相同,τy与τx的表达式结构相同。这种在水平方向上的各向同性是由悬挂线圈的悬挂机构的中心对称结构特性决定的;这种表达式反映的数学特性简化了分析过程,使得所有的力学分析只需要在一个平面内进行即可,另一个与之相垂直平面的情况可通过x,y相互替代得到。
式(10)~式(13)中的所有参数均可通过检测手段结合数学推导获取。
4.3水平位移与转角的测量方法
在获取水平安培力与电磁转矩的求解模型之后,还需测量线圈相对径向磁场的水平位移以及线圈的转角,为评估由水平安培力与电磁转矩做功引起的对准能量误差奠定基础。
采用线面式电容传感器[5]检测悬挂线圈相对径向磁场的水平位移。该电容传感器主要由一条镀金二氧化硅丝和一只外圆柱面黄铜极板组成,两者分别为电容传感器的高压极板和低压极板。其中镀金二氧化硅丝在测量时与静止的悬挂线圈固定一起,外圆柱面极板则被固定于运动的电磁体上;当电磁体在运动过程中发生相对于静止悬挂线圈的水平位移时,二氧化硅丝与外圆柱面极板之间的间距改变,其位移改变量被电容传感器后续处理电路测得。本实验所用的线面式电容传感器对水平位移的测量分辨力在测量距离小于5 mm(实际工作距离范围)的范围内约为0.05 μm。
采用3路激光干涉仪检测悬挂线圈的转角值。3个角锥棱镜作为干涉仪的测量目标被固定于悬挂线圈的下表面,且3个角锥棱镜均匀分布于360°方向上。3路激光干涉仪分别检测对应角锥棱镜所在线圈位置的垂向位移Δz。当线圈发生角度偏转,3路激光干涉仪测得的位移值都将发生改变,其改变量分别设为Δz1,Δz2,Δz3。则悬挂线圈转角的计算式可通过Δz1,Δz2,Δz3建立:

(14)
式中:r表示3个角锥棱镜在悬挂线圈位置的半径。本实验采用的激光干涉仪型号为美国Agilent公司的Agilent 5530激光位移测量干涉仪,其波长稳定性为±0.02×10-6,在空气环境下的测量精度为10-7量级,测量分辨力小于10 nm。
5 测量实验与误差评估
本节内容将对悬挂线圈相对于径向磁场的水平位移(x,y)和转角(θx,θy)进行检测,进而计算线圈所受水平安培力(Fx,Fy,)和电磁转矩(τy,τx)的值,并评估水平安培力与电磁转矩做功引起的对准能量误差。
5.1水平位移与转角的测量结果
图6所示为悬挂线圈相对于电磁体径向磁场的水平位移(x,y)测量结果。水平位移的产生原因主要有两点:首先,悬挂线圈通电后收到来自径向磁场的水平安培力作用,导致线圈水平位置改变;其次,电磁体沿垂向运动时存在微量水平位移,导致电磁体与线圈的水平间距改变。

图6 悬挂线圈相对于电磁体径向磁场的水平位移(x, y)测量结果
图7为悬挂线圈的转角(θx,θy)测量结果。悬挂线圈转角主要由转矩作用和电磁体运动时抖动共同作用产生。
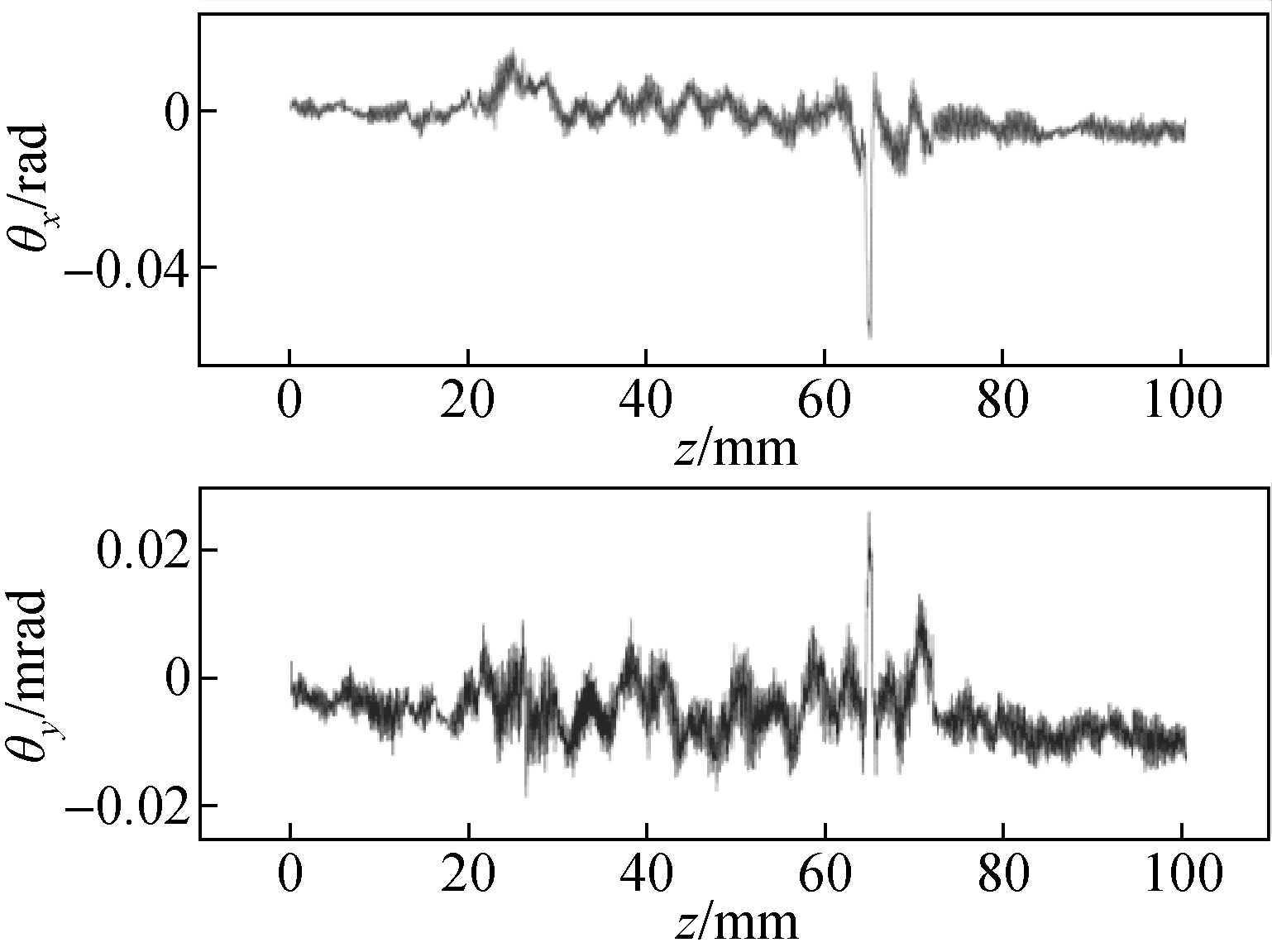
图7 悬挂线圈的转角(θx, θy)测量结果
5.2水平安培力和电磁转矩的计算结果
将x,y和θx,θy的测量结果代入式(10)~式(13)可求得Fx,Fy和τy,τx随垂向位置z的变化曲线如图8所示。

图8 水平安培力和电磁转矩的计算结果
5.3对准能量误差评估
不妨设水平安培力与电磁转矩做功量分别为WFx,WFy和Wτx,Wτy,其表达式为:
WFx=![]() Fxdx
Fxdx
WFy=![]() Fydy
Fydy
Wτx=![]() τxdθx
τxdθx
Wτy=![]() τydθy
τydθy
(15)
并设水平安培力与电磁转矩做功引起的对准能量误差为Wa,则其表达式为:
Wa=WFx+WFy+Wτx+Wτy
(16)
将Fx,Fy和τy,τx的计算值代入式(15)、式(16),可得对准能量误差Wa=2.7×10-7J,其相对对准误差为:
(17)
式中:Fz等于5 N;(z2-z1)等于40 mm。
6 结 论
能量天平线圈对准能量误差主要由水平安培力和电磁转矩做功引起。水平安培力和电磁转矩对线圈的作用效果均为驱使线圈以及其悬挂装置绕刀口支点位置摆动;为分别获取力与力矩的对应量值,设计了双柔性铰链解耦结构,实现了力与力矩在作用位置上的分离,并基于此分别建立了力与力矩的求解模型。通过对线圈相对于径向磁场的水平位移量和偏转角度的测量,以及对水平安培力和电磁转矩的求解,最终获取由水平安培力和电磁转矩做功引起的对准能量相对误差的评估量值约为1×10-6。
[1] Thomas M, Ziane D, Pinot P,etal. A determination of the Planck constant using the LNE Kibble balance in air[J].Metrologia, 2017,54(4): 468-480.
[2] Li Z, Zhang Z, Lu Y,etal. The Design and construction of the joule balance NIM-2[J].IEEETransactionsonInstrumentation&Measurement, 2017, 66(6):1 329-1 336.
[3] Li Z, Zhang Z, Lu Y,etal. The first determination of the Planck constant with the joule balance NIM-2[J].Metrologia, 2017, 54(5): 763-774.
[4] 张钟华,李辰,贺青,等.能量天平研究进展[J]. 计量学报,2014,35(4):305-310.
[5] Zeng T, Lu Y, Liu Y,etal. A capacitive sensor for the measurement of departure from the vertical movement[J].IEEETransactionsonInstrumentation&Measurement,2016, 65(2): 458-466.